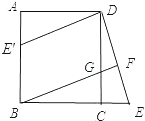
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.

(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
参考答案:
【答案】(1)见解析;(2)四边形E′BGD是平行四边形.
【解析】
试题分析:(1)由正方形ABCD,得BC=CD,∠BCD=∠DCE=90°,又CG=CE,所以△BCG≌△DCE(SAS).
(2)由(1)得BG=DE,又由旋转的性质知AE′=CE=CG,所以BE′=DG,从而证得四边形E′BGD为平行四边形.
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠BCD=90°.
∵∠BCD+∠DCE=180°,
∴∠BCD=∠DCE=90°.
又∵CG=CE,
∴△BCG≌△DCE.
(2)解:四边形E′BGD是平行四边形.理由如下:
∵△DCE绕D顺时针旋转90°得到△DAE′,
∴CE=AE′.
∵CE=CG,
∴CG=AE′.
∵四边形ABCD是正方形,
∴BE′∥DG,AB=CD.
∴AB﹣AE′=CD﹣CG.
即BE′=DG.
∴四边形E′BGD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李东同学参加校团委组织的演讲赛,共21名选手参赛,预赛成绩各不相同,按成绩取前10名的选手参加复赛,李东在知道自己成绩的情况下,要判断自己能否进入复赛,还需要知道这21名选手成绩的( )
A. 平均数 B. 方差 C. 众数 D. 中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】在弹性限度内,弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数.一根弹簧不挂物体时长15cm;当所挂物体的质量为5kg时,弹簧长20cm.所挂物体质量为8kg时弹簧的长度是_____cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
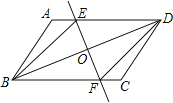
(1)求证:△DOE≌△BOF;
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是个缺水国家,目前可利用淡水资源总量仅约为899 000乙亿米3 , 其中数据899 000用科学记数法表示为( )
A.8.99×104
B.0.899×106
C.899×103
D.8.99×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】某天的最高温度是5℃,最低温度是-6℃,这一天温差是______℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(m﹣1)x2m﹣3=6是关于x的一元一次方程,则m的值是________.
相关试题

