【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求AD:EF的值.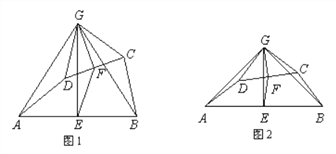
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)由线段垂直平分线的性质得出GA=GB,GD=GC,由SAS证明△AGD≌△BGC,得出对应边相等即可;
(2)先证出∠AGB=∠DGC,由![]() ,证出△AGB∽△DGC,得出比例式
,证出△AGB∽△DGC,得出比例式![]() ,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH,由△AGD≌△BGC,得出∠GAD=∠GBC,再求出∠AGB=∠AHB=90°,得出∠AGE=![]() ∠AGB=45°,求出
∠AGB=45°,求出![]() ,由△AGD∽△EGF,即可得出
,由△AGD∽△EGF,即可得出![]() 的值.
的值.
试题解析:(1)证明:∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
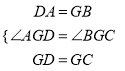 ,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)证明:∵∠AGD=∠BGC,
∴∠AGB=∠DGC,
在△AGB和△DGC中, ![]() ,
,
∴△AGB∽△DGC,
∴![]() ,
,
又∵∠AGE=∠DGF,
∴∠AGD=∠EGF,
∴△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,如图所示:
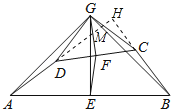
则AH⊥BH,
∵△AGD≌△BGC,
∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,
∴∠AGB=∠AHB=90°,
∴∠AGE=![]() ∠AGB=45°,
∠AGB=45°,
∴![]() ,
,
又∵△AGD∽△EGF,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每年11月的最后一个星期四是感恩节,小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人.他将调查结果分为如下四类:A类﹣﹣当面致谢;B类﹣﹣打电话;C类﹣﹣发短信息或微信;D类﹣﹣写书信.他将调查结果绘制成如图不完整的扇形统计图和条形统计图:

请你根据图中提供的信息完成下列各题:
(1)补全条形统计图;
(2)在A类的同学中,有3人来自同一班级,其中有1人学过主持.现准备从他们3人中随机抽出两位同学主持感恩节主题班会课,请你用树状图或表格求出抽出的两人都没有学过主持的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市购进一批文具袋,每个进价为8元.试销售期间,记录的每天的销售数量与销售单价的数据如下表:
销售单价x(元)
11
12
13
14
…
销售数量y(个)
34
32
30
28
…
备注:物价局规定,每个文具袋的售价不低于8元且不高于18元
(1)请你根据表中信息判断y是x的什么函数?求出其函数关系式,并写出自变量取值范围.
(2)有一天文具袋的销售单价为17元,不计其他因素,求该天销售文具袋的利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】七年级有新生x人,其中男生占45%,则该校七年级女生为人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①307000000用科学记数法可表示为
②85.90是精确到位的数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形BCPQ对角线交于点A,将一块等腰直角三角形中45°角的顶点放在A点,斜边AG所在的直线交BC于点D,直角边AH所在的直角交BC于点E.

(1)在边BC上取一点M,连接AM,AD平分∠BAM,求证:AE平分∠MAC;
(2)在(1)的条件下,请判断BD、CE、DE之间的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a﹣1|+(b+2)2=0,则(a+b)2012的值是 .
相关试题

