【题目】如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB=![]() , CD=2连接AC、AD、BD、BC,AD、CB分别交⊙O于E、F.
, CD=2连接AC、AD、BD、BC,AD、CB分别交⊙O于E、F.
(1)问四边形CEDF是何种特殊四边形?请证明你的结论;
(2)当AC与⊙O相切时,四边形CEDF是正方形吗?请说明理由.

参考答案:
【答案】(1)四边形CEDF是矩形(2)四边形CEDF是正方形.
【解析】试题分析:(1)根据对角线互相平分的四边形为平行四边形先判断四边形ADBC是平行四边形,根据平行四边形的性质可得CB∥AD,根据平行四边形的性质可得∠CFD+∠EDF=180°,再由直径所对的圆周角为直角,即可判断∠CFD=∠CED=∠EDF=90°,所以四边形CEDF是矩形;(2)由 AC是⊙O的切线,CD是直径,可得∠ACD=90°,在Rt△ACO中,OA=![]() ,OC=1,
,OC=1,![]() 求得AC =2,则CD=AC=2,∠CDE=45°,有因∠DEC=90°,DE=CE,即可判断矩形CEDF是正方形.
求得AC =2,则CD=AC=2,∠CDE=45°,有因∠DEC=90°,DE=CE,即可判断矩形CEDF是正方形.
试题解析:
(1)四边形CEDF是矩形.
证明:∵CD是⊙O的直径,
∴∠CFD=∠CED=90°,
∵CD⊙O的直径,
∴OC=OD,
∵OA=OB,
∴四边形ADBC是平行四边形,
∴CB∥AD,
∴∠CFD+∠EDF=180°,
∴∠EDF=90°,
∴四边形CEDF是矩形.
(2)四边形CEDF是正方形.
理由:∵AC是⊙O的切线,CD是直径,
∴∠ACD=90°,
在Rt△ACO中,OA=![]() ,OC=1,
,OC=1,![]() 5,
5,
∴AC=2,
则CD=AC=2,∠CDE=45°,
又∵∠DEC=90°
∴DE=CE,
∴矩形CEDF是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】在式子-3<0,x≥2,x=a,x2-2x,x≠3,x+1>y中,是不等式的有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+160元表示增加160元,那么﹣60元表示( )
A.增加100元
B.增加60元
C.减少60元
D.减少220元 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线
经过点E(1,0)和F(5,0),并交y轴于D(0,-5);抛物线 :
: (a≠0),
(a≠0),(1)试求抛物线
 的函数解析式;
的函数解析式;(2)求证: 抛物线
 与x轴一定有两个不同的交点;
与x轴一定有两个不同的交点;(3)若a=1
①抛物线
 、
、 顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线
顶点分别为 ( , )、( , ) ;当x的取值范围是_________ 时,抛物线 、
、 上的点的纵坐标同时随横坐标增大而增大;
上的点的纵坐标同时随横坐标增大而增大;②已知直线MN分别与x轴、
 、
、 分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。
分别交于点P(m,0)、M、N,且MN∥y轴,当1≤m≤5时,求线段MN的最大值。 -
科目: 来源: 题型:
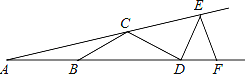
查看答案和解析>>【题目】如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=16cm,C是AB上一点,且AC=10cm,点D是线段AC的中点,点E是线段BC的中点.求线段DE的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P(1,1)位于( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
相关试题

