Question

【题目】（12分）在等腰△ABC中，AB=AC=2, ∠BAC=120°,AD⊥BC于D,点O、点P分别在射线AD、BA上的运动，且保证∠OCP=60°，连接OP.

（1）当点O运动到D点时，如图一，此时AP=______,△OPC是什么三角形。

（2）当点O在射线AD其它地方运动时，△OPC还满足（1）的结论吗？请用利用图二说明理由。

（3）令AO=x，AP=y，请直接写出y关于x的函数表达式，以及x的取值范围。

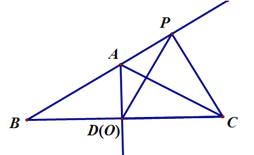
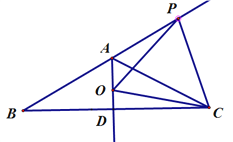
图一 图二

Answer 1

【答案】（1）1，等边三角形；（2）理由见解析；(3)当时，y=2-x；当时，

y=x-2

【解析】试题分析：（1）根据等腰三角形的性质得到∠B=∠ACB=30°，求得∠ACP=30°，根据全等三角形的性质即可得到结论；（2）过C作CE⊥AP于E，根据等边三角形的性质得到CD=CE，根据全等三角形的性质得到OC=OP，由等边三角形的判定即可得到结论；（3）分两种情况解决，在AB上找到Q点使得AQ=OA，则△AOQ为等边三角形，根据求得解实现的性质得到PA=BQ，求得AC=AO+AP，即可得到结论．

试题解析：

（1）AD=AP=1,

∵AB=AC=2，∠BAC=120°，

∴∠B=∠ACB=30°，

∵∠OCP=60°，

∴∠ACP=30°，

∵∠CAP=180°﹣∠BAC=60°，

∵AD⊥BC，

∴∠DAC=60°，

在△ADC与△APC中， ，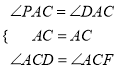

∴△ACD≌△ACP，

∴CD=CP，

∴△PCO是等边三角形；

（2）△OPC还满足（1）的结论，

理由：过C作CE⊥AP于E，

∵∠CAD=∠EAC=60°，

AD⊥CD，

∴CD=CE，

∴∠DCE=60°，

∴∠OCE=∠PCE，

在△OCD与△PCE中， ，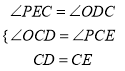

∴△OCD≌△PCE，

∴OC=OP，

∴△OPC是等边三角形；

（3）当0<x≤2时，

在AB上找到Q点使得AQ=OA，则△AOQ为等边三角形，

则∠BQO=∠PAO=120°，

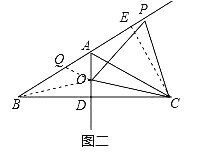
在△BQO和△PAO中， ，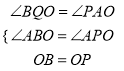

∴△BQO≌△PAO（AAS），

∴PA=BQ，

∵AB=BQ+AQ，

∴AC=AO+AP，

∵AO=x，AP=y，

∴y=﹣x+2；

当时， 利用同样的方法可求得y=x-2