【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
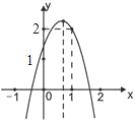
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】D
【解析】由抛物线的开口向下知a<0,
与y轴的交点为在y轴的正半轴上,得c>0,
对称轴为x=![]() <1,∵a<0,∴2a+b<0,
<1,∵a<0,∴2a+b<0,
而抛物线与x轴有两个交点,∴![]() 4ac>0,
4ac>0,
当x=2时,y=4a+2b+c<0,当x=1时,a+b+c=2.
∵![]() >2,∴4ac
>2,∴4ac![]() <8a,∴
<8a,∴![]() +8a>4ac,
+8a>4ac,
∵①a+b+c=2,则2a+2b+2c=4,②4a+2b+c<0,③ab+c<0.
由①,③得到2a+2c<2,由①,②得到2ac<4,4a2c<8,
上面两个相加得到6a<6,∴a<1.故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtABC 中, BAC 90, AB AC ,点 D 是 AB 的中点,AF CD 于 H 交 BC 于 F, BE AC 交 AF 的延长线于 E.
求证:(1)ADC ≌ BEA
(2)BC 垂直平分 DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A、B分别在x轴、y轴上,点A与点C关于y轴对称,点E是线段AC上的点(点E不与点A、C重合)
(1)若点A的坐标为(a,0),则点C的坐标为 ;
(2)如图1,点F是线段AB上的点,若∠BEF=∠BAO,∠BAO=2∠OBE,求证:AF=CE;
(3)如图2,若点D为AC上一点,连接ED,满足BE=BD,试探究∠ABE与∠DEC的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=
 BF;④AE=BG.其中正确的个数是( )
BF;④AE=BG.其中正确的个数是( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A1的坐标为(0,1),直线1为y=x.过点A1作A1B1⊥y轴交直线1于点B1,过点B1作A2B1⊥1交y轴于点A2;过点A2作A2B2⊥y轴交直线1于点B2,过点B2作A3B2⊥1交y轴于点A3,……,则AnBn的长是______.
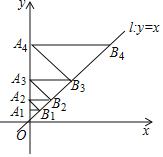
-
科目: 来源: 题型:
查看答案和解析>>【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.

(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式,探究其中规律.
第1个等式:
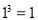 ;
;第2个等式:
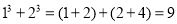
第3个等式:
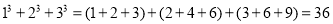
……
(1)第4个等式:
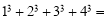 (直接填写结果);
(直接填写结果);(2)根据以上规律请计算:
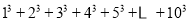 ;
;(3)通过以上规律请猜想写出:
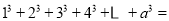 (直接填写结果).
(直接填写结果).
相关试题

