【题目】已知关于x的二次函数y=x2+（k2﹣3k﹣4）x+2k的图象与x轴从左到右交于A，B两点，且这两点关于原点对称．

（1）求k的值；

（2）在（1）的条件下，若反比例函数y=的图象与二次函数y=x2+（k2﹣3k﹣4）x+2k的图象从左到右交于Q，R，S三点，且点Q的坐标为（﹣1，﹣1），点R（xR，yR），S（xs，ys）中的纵坐标yR，ys分别是一元二次方程y2+my﹣1=0的解，求四边形AQBS的面积S四边形AQBS；

（3）在（1），（2）的条件下，在x轴下方是否存在二次函数y=x2+（k2﹣3k﹣4）x+2k图象上的点P使得S△PAB=2S△RAB？若存在，求出点P的坐标；若不存在，请说明理由．

参考答案：

【答案】（1）－1；（2）；（3）不存在，理由见解析

【解析】试题分析：（1）设A点坐标为（x1，0），B点坐标为（x2，0），由A、B两点关于原点对称，即可得x1+x2=0，又由x1+x2=﹣（k2﹣3k﹣4），即可求得k的值；

（2）由Q点的坐标求出m的值，从而确定一元二次方程y2﹣my﹣1=0即为y2+y﹣1=0，解得：y= ，因为点R在点S的左边，所以yR= ，由（1）得二次函数y=x2﹣2，令x2﹣2=0，解得：x1=-,x2=，所以A（﹣，0），B（，0），即可求得AB的长，又由四边形AQBS的面积为：S△AQB+S△ASB求得答案；

（3）由抛物线的顶点坐标为（0，﹣2），假设满足条件的点P存在，由S△PAB=2S△RAB，可得点P的纵坐标，即可得即在x轴下方抛物线上不存在点P，使S△PAB=2S△RAB．

试题解析：

（1）设A点坐标为（x1，0），B点坐标为（x2，0），

∵A、B两点关于原点对称，

∴x1+x2=0，

又x1+x2=﹣（k2﹣3k﹣4），

则k2﹣3k﹣4=0，

解得k1=﹣1，k2=4，

当k=4时，抛物线为y=x2+8，此时△=﹣32＜0，舍去；

当k=﹣1时，抛物线为y=x2﹣2，此时△=8＞0，则抛物线与x轴交于两点，

故所求k值为﹣1．

（2）如图：

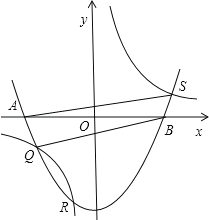
∵Q的坐标为（﹣1，﹣1），在y=上，

∴-1= ，

解得：m=1，

∴一元二次方程y2﹣my﹣1=0即为y2+y﹣1=0，

解得：y= ，

∵点R在点S的左边，

∴yR=，

由（1）得二次函数y=x2﹣2，令x2﹣2=0，解得：x1=-,x2=，

∴A（﹣，0），B（，0），

∴AB=|-(-)|=2，

则四边形AQBS的面积为：

S△AQB+S△ASB=

（3）∵抛物线的顶点坐标为（0，﹣2），假设满足条件的点P存在，

则∵S△PAB=2S△RAB，

∴点P的纵坐标为：2×（）=﹣1- ，

而﹣1﹣，

∴P点不存在．

即在x轴下方抛物线上不存在点P，使S△PAB=2S△RAB．

关闭