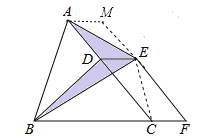
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且![]() ,四边形DCFE是平行四边形,则图中阴影部分的面积为( ).
,四边形DCFE是平行四边形,则图中阴影部分的面积为( ).
A.3 B.4 C.6 D.8

参考答案:
【答案】A
【解析】
试题分析:连接EC,过A作AM∥BC交FE的延长线于M,
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE边DE上的高和△CDE的边DE上的高相同,
∴△BDE的面积和△CDE的面积相等,
同理△ADE的面积和△AME的面积相等,
即阴影部分的面积等于平行四边形ACFM的面积的一半,是![]() ×
×![]() CF×hCF,
CF×hCF,
∵△ABC的面积是24,BC=4CF
∴![]() BC×hBC=
BC×hBC=![]() ×4CF×hCF=24,
×4CF×hCF=24,
∴CF×hCF=12,
∴阴影部分的面积是![]() ×
×![]() ×12=3,
×12=3,
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是△ABC的两条角平分线的交点,若∠BOC=110°,则∠A=______°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.
(1)求证:△DEC≌△EDA;(2)求DF的值;(3)在线段AB上找一点P,连结FP使FP⊥AC,连结PC,试判定四边形APCF的形状,并说明理由,直接写出此时线段PF的大小

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=(m﹣n)x2+mx+n是二次函数的条件是( )
A.m、n是常数,且m≠0
B.m、n是常数,且m≠n
C.m、n是常数,且n≠0
D.m、n可以为任何常数 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
(1)将△ABC沿x轴翻折后再沿x轴向右平移1个单位,在图中画出平移后的△AB1C1。若△ABC内有一点P(a,b),则经过两次变换后点P的坐标变为_____________
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
(3) 若将△ABC绕某点逆时针旋转90°后,其对应点分别为
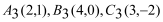 ,则旋转中心坐标为_________.
,则旋转中心坐标为_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,E,M,N分别是AB,AC,BC的中点,CF∥AB,连接MN,连接并延长EM,与直线CF交于F,连接FN交直线AB于点D,交AC于O点.
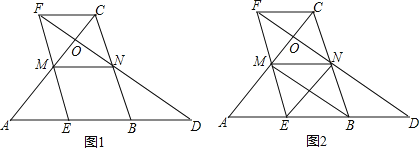
(1)如图(1),BA=BC,求证:四边形FMNC为菱形;
(2)如图(2),连接MB,NE,在不添加任何辅助线的情况下,请直接写出图(2)中的所有平行四边形(BE为边的除外).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 ________.

相关试题

