【题目】如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π) 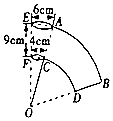
参考答案:
【答案】解:由题意可知: ![]() =6πcm,
=6πcm, ![]() =4π,设∠AOB=n,AO=R,则CO=R﹣9, 由弧长公式得:l=
=4π,设∠AOB=n,AO=R,则CO=R﹣9, 由弧长公式得:l= ![]() ,
,
∴ ![]() ,
,
解得:n=40,R=27,
故扇形OAB的圆心角是40度.
∵R=27,R﹣9=18,
∴S扇形OCD= ![]() ×4π×18=36π(cm2),
×4π×18=36π(cm2),
S扇形OAB= ![]() ×6π×27=81π(cm2),
×6π×27=81π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=81π﹣36π=45π(cm2),
纸杯底面积=π22=4π(cm2)
纸杯表面积=45π+4π=49π(cm2).
【解析】(1)设∠AOB=n°,AO=R,则CO=R﹣9,利用圆锥的侧面展开图扇形的弧长等于圆锥底面周长作为相等关系列方程,并联立成方程组求解即可(2)求纸杯的侧面积即为扇环的面积,需要用大扇形的面积减去小扇形的面积.纸杯表面积=S纸杯侧面积+S纸杯底面积 .
【考点精析】通过灵活运用几何体的展开图和扇形面积计算公式,掌握沿多面体的棱将多面体剪开成平面图形,若干个平面图形也可以围成一个多面体;同一个多面体沿不同的棱剪开,得到的平面展开图是不一样的,就是说:同一个立体图形可以有多种不同的展开图;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
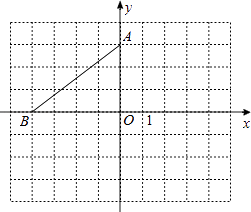
(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.
(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】图中标明了小英家附近的一些地方,已知游乐场的坐标为(3,2).
(1)在图中建立平面直角坐标系,并写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2),(3,-1),(1,-1),(-1,-2),(-3,-1)的路线转了一下,又回到家里,写出路上她经过的地方.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
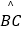 的中点.
的中点. 
(1)求证:AB=BC;
(2)求证:四边形BOCD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个运算装置,当输入值为x时,其输出值为y,且y是x的二次函数,已知输入值为﹣2,0,1时,相应的输出值分别为5,﹣3,﹣4.
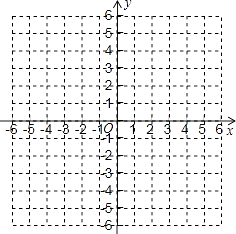
(1)求此二次函数的解析式;
(2)在所给的坐标系中画出这个二次函数的图象,并根据图象写出当输出值y为正数时输入值x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

相关试题

