【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向东南方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后在C处成功拦截不明船只,问我国海监执法船在前往监视巡查的过程中行驶了多少海里?

参考答案:
【答案】即我海监执法船在前往监视巡查的过程中行驶了![]() 海里.
海里.
【解析】试题分析:过B作BD⊥AC,在Rt△ABD中,利用勾股定理求出BD与AD的长,在Rt△BCD中,求出CD的长,由AD+DC求出AC的长即可.
试题解析:
过B作BD⊥AC,

∵∠BAC=75°﹣30°=45°,
∴在Rt△ABD中,∠BAD=∠ABD=45°,∠ADB=90°,
由勾股定理得:BD=AD=![]() ×20=10
×20=10![]() (海里),
(海里),
在△ABC中, ∠BAC=45°,∠ABC=75°,可得∠C=60°
∴在Rt△CBD中,
∴tan∠BCD =![]() ,即tan60°=
,即tan60°=![]() ,即CD=
,即CD=![]()
则AC=AD+DC=10![]() +
+![]()
答:即我海监执法船在前往监视巡查的过程中行驶了10![]() +
+![]() 海里.
海里.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.

(1)若∠BAE=40°,求∠C的度数;
(2)若△ABC周长13cm,AC=6cm,求DC长. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于圆的周长公式C=2πr,下列说法正确的是 ( )
A. C,r是变量,2是常量 B. r是变量,C是常量
C. C是变量,r是常量 D. C,r是变量,2π是常量
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,以便国家精准扶贫政策有效落实.统计发现班上贫困家庭学生人数分别有2名、3名、4名、5名、6名,共五种情况.并将其制成了如下两幅不完整的统计图:
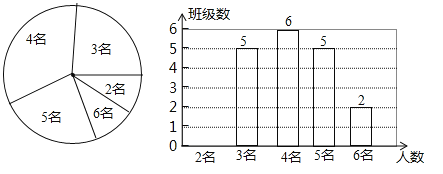
(1)求该校一共有多少个班?并将条形图补充完整;
(2)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是__________,依次继续下去……第2 016次输出的结果是___________.

相关试题

