【题目】甲从A地出发步行到B地,乙同时从B地步行出发至A地,2小时后在中途相遇,相遇后,甲、乙步行速度都提高了1千米/小时.若设甲刚出发时的速度为a千米/小时,乙刚出发的速度为b千米/小时.
(1)A、B两地的距离可以表示为 千米(用含a,b的代数式表示);
(2)甲从A到B所用的时间是: 小时(用含a,b的代数式表示);
乙从B到A所用的时间是: 小时(用含a,b的代数式表示).
(3)若当甲到达B地后立刻按原路向A返行,当乙到达A地后也立刻按原路向B地返行.甲乙二人在第一次相遇后3小时36分钟又再次相遇,请问AB两地的距离为多少?
参考答案:
【答案】(1)2(a+b);(2)(2+![]() );(2+
);(2+![]() );(3)36.
);(3)36.
【解析】
(1)根据两地间的距离=两人的速度之和×第一次相遇所需时间,即可得出结论;
(2)利用时间=路程÷速度结合2小时后第一次相遇,即可得出结论;
(3)设AB两地的距离为S千米,根据路程=速度×时间,即可得出关于(a+b),S的二元一次方程组(此处将a+b当成一个整体),解之即可得出结论.
(1)A、B两地的距离可以表示为2(a+b)千米.
故答案为:2(a+b).
(2)甲乙相遇时,甲已经走了![]() 千米,乙已经走了
千米,乙已经走了![]() 千米,
千米,
根据相遇后他们的速度都提高了1千米/小时,得甲还需![]() 小时到达B地,乙还需
小时到达B地,乙还需![]() 小时到达A地,
小时到达A地,
所以甲从A到B所用的时间为(2+![]() )小时,乙从B到A所用的时间为(2+
)小时,乙从B到A所用的时间为(2+![]() )小时.
)小时.
故答案为:(2+![]() );(2+
);(2+![]() ).
).
(3)设AB两地的距离为S千米,3小时36分钟=![]() 小时.
小时.
依题意,得:  ,
,
令x=a+b,则原方程变形为 ,
,
解得:![]() .
.
答:AB两地的距离为36千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有M、N两点,M点表示的数分别为m,N点表示的数是n(n>m),则线段MN的长(点M到点N的距离)可表示为MN=n﹣m,请用上面材料中的知识解答下面的问题:一个点从数轴上的原点O开始,先向左移动3cm到达A点,再向右移动2cm到达B点,然后向右移动4cm到达C点,用1cm表示1个单位长度.
(1)请你在数轴上表示出A、B、C三点的位置,并直接写出线段AC的长度.
(2)若数轴上有一点D,且AD=4cm,则点D表示的数是什么?
(3)若将点A向右移动xcm,请用代数式表示移动后的点所表示的数.
(4)若点P以从点A向原点O移动,同时点Q以与点P相同的速度从原点O向点C移动,试探索:PQ的长是否会发生改变?如果不变,请求出PQ的长.如果改变,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3
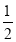 的值;
的值;(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接一个对角线互相垂直的四边形各边中点,所得的四边形是 形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图方式放置,点A1、A2、A3…和点C1、C2、C3…分别在直线
 和x轴上。已知点B1(1,1)、B2(3,2),请写出点B3的坐标是___________,点Bn的坐标是_______________。
和x轴上。已知点B1(1,1)、B2(3,2),请写出点B3的坐标是___________,点Bn的坐标是_______________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要从小王和小李两名同学中挑选一人参加全市知识竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
次数
1
2
3
4
5
小王
60
75
100
90
75
小李
70
90
100
80
80
根据上表解答下列问题:
(1)完成下表:
姓名
平均成绩(分)
中位数(分)
众数(分)
方差
小王
80
75
75
190
小李
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王、小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为选谁参加比赛比较合适?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线y=x+b与双曲线y=
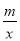 的一个交点为A(2,4),与y轴交于点B.
的一个交点为A(2,4),与y轴交于点B.(1)求m的值和点B的坐标;
(2)点P在双曲线y=
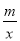 上,△OBP的面积为8,直接写出点P的坐标.
上,△OBP的面积为8,直接写出点P的坐标.
相关试题

