【题目】如图,平面直角坐标系xOy中,一次函数y=﹣![]() x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
x+b(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.

(1)若直线AB与![]() 有两个交点F、G.
有两个交点F、G.
①求∠CFE的度数;
②用含b的代数式表示FG2,并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)45°;(2)4≤b<5;(3)存在 P(![]() ,
, ![]() ).
).
【解析】试题分析:(1)①∠EOC和∠EFC是![]() 所对的圆心角和圆周角,根据同弧所对的圆周角是圆心角的一半进行求解即可;
所对的圆心角和圆周角,根据同弧所对的圆周角是圆心角的一半进行求解即可;
②过O作OM⊥FG于点M,连接OF,先求出一次函数图像与x轴、y轴交点A、B的坐标,然后根据勾股定理求出AB的长,进而利用面积法求出OM的长,再利用勾股定理表示出FM2,再由垂径定理得FG=2FM,进而可以表示出FG2,再根据式子写出b的范围;
(2)根据前面结论OM=![]() ,当b>5时,直线与圆相离,当b=5时,直线与圆相切,连接OP,根据两直线垂直时比例系数的积为-1求出OP的解析式,然后联立两个解析式即可求出点P的坐标.
,当b>5时,直线与圆相离,当b=5时,直线与圆相切,连接OP,根据两直线垂直时比例系数的积为-1求出OP的解析式,然后联立两个解析式即可求出点P的坐标.
试题解析:
解:(1)①∵∠COE=90°,
∴∠CFE=![]() ∠COE=45°;
∠COE=45°;
②如图,作OM⊥AB点M,连接OF,
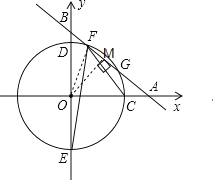
∵直线的函数式为:y=![]() ,
,
∴B的坐标为(0,b),A的坐标为(![]() ,0),
,0),
∴AB=![]()
=![]() ,
,
在Rt△OBC中,由面积法可得
OA·OB=AB·OM,
易得:OM=![]() ,
,
∵OF=4,
∴FM2=OF2﹣OM2=42﹣(![]() )2 ,
)2 ,
∵OM⊥FG,
∴FG=2FM,
∴FG2=4FM2=4×[42﹣(![]() )2 ]=64﹣
)2 ]=64﹣![]() b2,
b2,
∵直线AB与![]() 有两个交点F、G.
有两个交点F、G.
∴4≤b<5;
(2)存在.
如图,
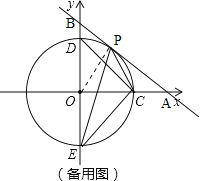
当b>5时,OM=![]() >4,∴直线与圆相离,∠CPE<45°;
>4,∴直线与圆相离,∠CPE<45°;
当b=5时,OM=![]() =4,∴直线与圆相切,
=4,∴直线与圆相切,
∵DE是直径,
∴∠DCE=90°,
∵CO⊥DE,且DO=EO,
∴∠ODC=∠OEC=45°,
∴∠CPE=∠ODC=45°,
∴存在点P,使∠CPE=45°,
连接OP,
∵P是切点,∴OP⊥AB,∴OP所在的直线为:y=![]() ,
,
又∵AB所在的直线为:y=![]() +5,
+5,
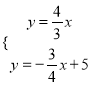
解得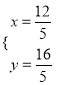
∴P(![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图(2),∠BDC的平分线分别交AC,BC于点E,F,求∠CEF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式,结果为﹣9a6b﹣4的是( )
A.(﹣3a3b﹣2)2
B.﹣(3a4b﹣2)2
C.﹣(3a4b﹣6)2
D.﹣(3a3b﹣2)2 -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三家超市为促销一种定价相同的商品,甲超市先降价20%,后又降价10%;乙超市连续两次降价15%;丙超市一次降价30%.则顾客到哪家超市购买这种商品更合算( )
A. 甲B. 丙C. 乙D. 一样
-
科目: 来源: 题型:
查看答案和解析>>【题目】若5x=125y , 3y=9z , 则x:y:z等于( )
A.1:2:3
B.3:2:1
C.1:3:6
D.6:2:1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数a,b满足a+b=2,a﹣b=5,则(a+b)3(a﹣b)3的值是 .
相关试题

