【题目】某家庭农场要建一个长方形的养兔场,兔场的两边靠墙(两堵墙互相垂直,长度不限),另两边用木栏围成,木栏总长20米.
(1)兔场的面积能达到100平方米吗?请你给出设计方案;
(2)兔场的面积能达到110平方米吗?如能,请给出设计方案,若不能说明理.

参考答案:
【答案】(1)10 m;(2)110 m2.
【解析】试题分析:(1)设AB=x,则BC=20–x,利用矩形的面积作为等量关系列方程,解方程求解即可,根据方程解的情况给出方案;(2)设AB=x,则BC=20–x,利用矩形的面积作为等量关系列方程,若一元二次方程有解则可求出长和宽从而可设计方案,若方程无解,则不能围成上述条件的长方形.
试题解析:
(1)设AB=x,则BC=20–x,根据题意,得x(20–x)=100
整理,得x2–20x+100=0,
解得x1=x2=10,
所以兔场的面积能达到100 m2,
设计方案为:AB=BC=10 m.
(2)设AB=x,则BC=20–x,根据题意,得x(20–x)=110,
整理,得x2–20x+110=0,∵Δ=400–440<0,∴原方程无解.
故兔场的面积不能达到110 m2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形有两条边的长度分别是5和7,则最长边a的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:m2﹣1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】25的平方根是( )
A. ±5 B. 5 C. ﹣5 D. ±25
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.x+x=x2
B.x6÷x2=x3
C.xx3=x4
D.(2x2)3=6x5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣ab=20,ab﹣b2=﹣12,则a2﹣b2= , a2﹣2ab+b2= .
-
科目: 来源: 题型:
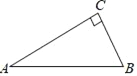
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°.
(1)用圆规和直尺在AC上作点P,使点P到A、B的距离相等.(保留作图痕迹,不写作法和证明)
(2)当满足(1)的点P到AB、BC的距离相等时,求∠A的度数.
相关试题

