Question

【题目】如图，在正方形ABCD中，连接BD，点O是BD的中点，若M、N是边AD上的两点，连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有（ ）

A.2对
B.3对
C.4对
D.5对

Answer 1

【答案】C
【解析】解：∵四边形ABCD是正方形，
∴AB=CD=CB=AD，∠A=∠C=∠ABC=∠ADC=90°，AD∥BC，
在△ABD和△BCD中，
，
∴△ABD≌△BCD，
∵AD∥BC，
∴∠MDO=∠M′BO，
在△MOD和△M′OB中，
，
∴△MDO≌△M′BO，同理可证△NOD≌△N′OB，∴△MON≌△M′ON′，
∴全等三角形一共有4对．
故选C．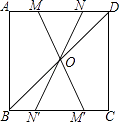

可以判断△ABD≌△BCD，△MDO≌△M′BO，△NOD≌△N′OB，△MON≌△M′ON′由此即可对称结论．本题考查正方形的性质、全等三角形的判定和性质，解题的关键是熟练掌握全等三角形的判定方法，属于基础题，中考常考题型．