【题目】已知二次函数y=x2-2x-3的图象与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)求点A、B、C、D的坐标.
(2)说出抛物线y=x2-2x-3可由抛物线y=x2如何平移得到?
(3)求四边形OCDB的面积.
参考答案:
【答案】(1)A(﹣1,0),B(3,0),C(0,﹣3),D(1,﹣4)图形见解析;
(2)抛物线y=x2-2x-3可由y=x2先向右平移1个单位,再向下平移4个单位而得到;
(3)四边形OCDB的面积为![]() .
.
【解析】试题分析:(1)先把此二次函数化为y=(x+1)(x﹣3)的形式,即可求出A、B两点的坐标,由二次函数的解析式可知c=﹣3,故可知C点坐标,由二次函数的顶点式即可求出其顶点坐标;
(2)根据四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED即可解答.
试题解析:(1)∵二次函数y=x2﹣2x﹣3可化为y=(x+1)(x﹣3),A在B的左侧,
∴A(﹣1,0),B(3,0),
∵c=﹣3,
∴C(0,﹣3),
∵x=![]() =
=![]() =1,y=
=1,y=![]() =﹣4,
=﹣4,
∴D(1,﹣4),故此函数的大致图象为:
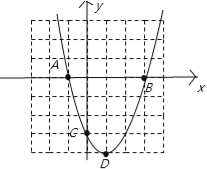
(2)抛物线y=x2-2x-3可由y=x2先向右平移1个单位,再向下平移4个单位而得到;
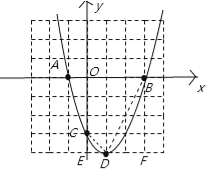
(3)连接CD、BD,
则四边形OCDB的面积=S矩形OEFB﹣S△BDF﹣S△CED
=OB|OE|﹣![]() DF|BF|﹣
DF|BF|﹣![]() DECE
DECE
=3×4﹣![]() ×2×4﹣
×2×4﹣![]() ×1×1
×1×1
=12﹣4﹣![]()
=![]() .
.
 .
.
考点:二次函数图象上点的坐标特征.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4290元,且销售完这批商品后获利多于1260元,请问共有几种购货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据已知求值.
(1)已知3×9m×27m=316 , 求m的值.
(2)已知am=2,an=5,求a2m﹣3n的值.
(3)已知2x+5y﹣3=0,求4x32y的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. 2a+b=3ab B. 2b3+3b3=5b6 C. 6a3﹣2a3=4 D. 5a2b﹣4a2b=a2b
-
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=2x2﹣8x+9,化成y=a(x﹣h)2+k的形式是:___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若将点A(1,3)向左平移2个单位,再向下平移4个单位得到点B,则点B的坐标为( )
A.(﹣2,﹣1)
B.(﹣1,0)
C.(﹣1,﹣1)
D.(﹣2,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a、b、c在数轴上的位置如图所示,求|a+c|﹣|c﹣b|﹣|a+b|值.
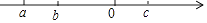
相关试题

