【题目】计算下面各题.
(1)计算: ![]() +(1﹣
+(1﹣ ![]() )0﹣4cos45°.
)0﹣4cos45°.
(2)解方程组: ![]() .
.
参考答案:
【答案】
(1)解:原式= ![]() +1﹣4×
+1﹣4× ![]() ,
,
=2 ![]() +1﹣2
+1﹣2 ![]() ,
,
=1.
(2)解:方程①×2+②得:3x=9,
方程两边同时除以3得:x=3,
将x=3代入①中得:3﹣y=2,
移项得:y=1.
∴方程组的解为 ![]()
【解析】(1)由a0=1以及特殊角的三角函数值,可得出(1﹣ ![]() )0=1,cos45°=
)0=1,cos45°= ![]() ,将其代入算式中即可得出结论;(2)根据用加减法解二元一次方程组的步骤解方程组即可得出结论.
,将其代入算式中即可得出结论;(2)根据用加减法解二元一次方程组的步骤解方程组即可得出结论.
【考点精析】解答此题的关键在于理解零指数幂法则的相关知识,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数),以及对解二元一次方程组的理解,了解二元一次方程组:①代入消元法;②加减消元法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
(1)请在如图所示的网格平面内作出平面直角坐标系,使点A坐标为(1,3)点B坐标为(2,1);
(2)请作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标;
(3)判断△ABC的形状.并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=x+1的图象与y轴交于点A,一次函数y2=kx+b的图象经过点B(0,3),且分别与x轴及y1=x+1的图象交于点C,D,点D的横坐标为
 .
.(1)求k,b的值;
(2)当x_____时,y2>0;
(3)若在一次函数y1=x+1的图象上有一点E(
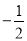 ,n),将点E向右平移2个单位后,得对应点E',判断点E'是否在一次函数y2=kx+b的图象上.
,n),将点E向右平移2个单位后,得对应点E',判断点E'是否在一次函数y2=kx+b的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.

(1)求线段BC的长;
(2)求线段MN的长;
(3)若C在线段AB延长线上,且满足AC﹣BC=b cm,M,N分别是线段AC,BC的中点,你能猜想MN的长度吗?请写出你的结论(不需要说明理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在落实国家“营养餐”工程中,选用了A,B,C,D种不同类型的套餐.实行一段时间后,学校决定在全校范围内随机抽取部分学生对“你喜欢的套餐类型(必选且只选一种)”进行问卷调查,将调查情况整理后,绘制成如图所示的两个统计图.
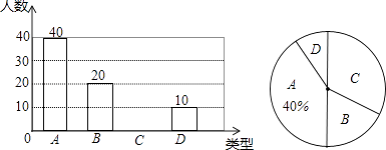
请你根据以上信息解答下列问题:
(1)在这次调查中,一共抽取了名学生;
(2)请补全条形统计图;
(3)如果全校有1200名学生,请你估计其中喜欢D套餐的学生的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整2h后提速行驶至乙地.设行驶时间为x( h),货车的路程为y1( km),小轿车的路程为y2( km ),图中的线段OA与折线OBCD分别表示y1,y2与x之间的函数关系.
(1)甲乙两地相距_____km,m=_____;
(2)求线段CD所在直线的函数表达式;
(3)小轿车停车休整后还要提速行驶多少小时,与货车之间相距20km?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠BAC=45°,AD⊥BC于点D,BE⊥AC于点E,且与AD交于点F.G是边AB的中点,连接EG交AD于点H.
(1)求证:△AEF≌△BEC;
(2)求证:CD=
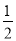 AF;
AF;(3)若BD=2,求AH的长.

相关试题

