【题目】某中学数学兴趣小组为了解本校学生对电视节目的喜爱情况,随机调查了部分学生最喜爱哪一类节目 (被调查的学生只选一类并且没有不选择的),并将调查结果制成了如下的两个统计图(不完整).请你根据图中所提供的信息,完成下列问题:
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出新闻节目在扇形统计图中所占圆心角的度数;
(3)若该中学有3000名学生,请估计该校喜爱电视剧节目的人数.
参考答案:
【答案】
(1)
解:本次调查的总人数是69÷23%=300(人)
(2)
解:B种类的人数是300×20%=60(人),
C类所占的百分比是 ![]() =30%.
=30%.
 ;
;
新闻节目在扇形统计图中所占圆心角的度数为360°×12%=43.2°
(3)
解:3000×23%=690(人).
答:估计该校喜爱电视剧节目的人数是690人
【解析】(1)根据A类的人数是69,所占的百分比是23%,据此即可求得调查的总人数;(2)根据百分比的意义求得B类的人数和C类所占的百分比补全直方图和扇形统计图,利用360°乘以对应的百分比求得新闻节目在扇形统计图中所占圆心角的度数;(3)利用总人数3000乘以对应的百分比即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数n
100
150
200
500
800
1000
摸到白球的次数m
59
96
116
290
480
601
摸到白球的频率

a
0.64
0.58
b
0.60
0.601
(1)上表中的a=;b=
(2)“摸到白球”的概率的估计值是(精确到0.1);
(3)试估算口袋中黑、白两种颜色的球各有多少只? -
科目: 来源: 题型:
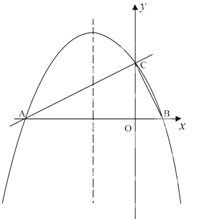
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,直线
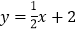 与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是
与x 轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是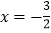 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B. (1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(a﹣3b)(a+3b)﹣(﹣a﹣2b)(a﹣2b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】九台区中小学生大约有8.9万人,近似数8.9万精确到位.
-
科目: 来源: 题型:
查看答案和解析>>【题目】x3﹣4x分解因式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2x+k﹣1=0有两个不相等的实数根,求k的取值范围.
相关试题

