搜索
【题目】某社区有一块空地需要绿化，某绿化组承担了此项任务，绿化组工作一段时间后，提高了工作效率，该绿化组完成的绿化面积 S（单位：m2）与工作时间 t（单位：h）之间的函数关系 如图所示，则该绿化组提高工作效率前每小时完成的绿化面积是（ ）
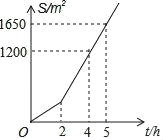
A. 150 m2 B. 300 m2 C. 330 m2 D. 450 m2
参考答案：
【答案】A
【解析】
根据待定系数法可求直线AB的解析式，再根据函数上点的坐标特征得出当x=2时，y的值，再根据工作效率=工作总量÷工作时间，列出算式求出该绿化组提高工作效率前每小时完成的绿化面积．
如图，
设直线AB的解析式为y=kx+b，则
，
解得
，
故直线AB的解析式为y=450x﹣600，
当x=2时，y=450×2﹣600=300，
300÷2=150（m2），
即该绿化组提高工作效率前每小时完成的绿化面积是150m2，
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB、AC边的垂直平分线分别交BC边于点M、N．
(1)如图①，若△AMN是等边三角形，则∠BAC= °；
(2)如图②，若∠BAC=135°，求证：BM2+CN2=MN2．
(3)如图③，∠ABC的平分线BP和AC边的垂直平分线相交于点P，过点P作PH垂直BA的延长线于点H．若AB=4，CB=10，求AH的长．
-
科目： 来源： 题型：
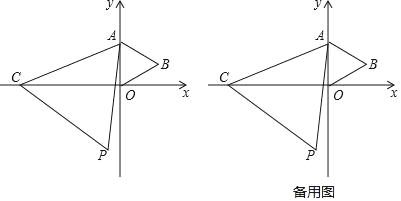
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，点A的坐标是（0，2），点C是x轴上的一个动点．当点C在x轴上移动时，始终保持△ACP是等边三角形（点A、C、P按逆时针方向排列）；当点C移动到点O时，得到等边三角形AOB（此时点P与点B重合）．
初步探究
(1)写出点B的坐标 ；
(2)点C在x轴上移动过程中，当等边三角形ACP的顶点P在第三象限时，连接BP，求证：△AOC≌△ABP．
深入探究
(3)当点C在x轴上移动时，点P也随之运动．探究点P在怎样的图形上运动，请直接写出结论；并求出这个图形所对应的函数表达式．
拓展应用
(4)点C在x轴上移动过程中，当△POB为等腰三角形时，直接写出此时点C的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E，如果∠BAC=60°，∠ACE=24°，那么∠BCE的大小是（ ）
A. 24° B. 30° C. 32° D. 36°
-
科目： 来源： 题型：
查看答案和解析>>【题目】三种不同类型的地砖的长、宽如图所示，若现有A型地砖4块，B型地砖4块，C型地砖2块，要拼成一个正方形，则应去掉1块________型地砖；这样的地砖拼法可以得到一个关于m，n的恒等式为____________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知直线
与x、y轴交于B、C两点，A（0，0），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第n个等边三角形的边长等于（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
(1)(－10xy3)·2xy4z；
(2)(－4x)(2x2－2x－1);
(3)0.4x2y·
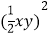－(－2x)3·xy3；(4)－3a
＋2b(a2－ab)－2a2(b＋3)．
相关试题
