【题目】如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
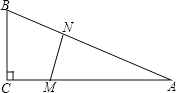
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
参考答案:
【答案】(1)当t为4时,∠AMN=∠ANM.(2)当t=6时,S最大值=![]() 平方米.
平方米.
【解析】
试题分析:(1)用t表示出AM和AN的值,根据AM=AN,得到关于t的方程求得t值即可;
(2)作NH⊥AC于H,证得△ANH∽△ABC,从而得到比例式,然后用t表示出NH,从而计算其面积得到有关t的二次函数求最值即可.
解:(1)∵从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
∴AM=12﹣t,AN=2t
∵∠AMN=∠ANM
∴AM=AN,从而12﹣t=2t
解得:t=4 秒,
∴当t为4时,∠AMN=∠ANM.
(2)在Rt△ABC中
∵AB2=BC2+AC2
∴AB=13米
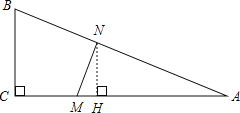
如图,作NH⊥AC于H,
∴∠NHA=∠C=90°,
∵∠A是公共角,
∴△NHA∽△BCA
∴![]() =
=![]() ,
,
即:![]() =
=![]() ,
,
∴NH=![]()
从而有S△AMN=![]() (12﹣t)
(12﹣t)![]() =﹣
=﹣![]() t2+
t2+![]() ,
,
∴当t=6时,S最大值=![]() 平方米.
平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线,下列结论:
①△ABD,△BCD都是等腰三角形;
②AD=BD=BC;
③BC2=CDCA;
④D是AC的黄金分割点
其中正确的是( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
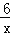 (x>0)的图象交于A(m,6),B(3,n)两点
(x>0)的图象交于A(m,6),B(3,n)两点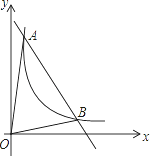
(1)求一次函数的解析式;
(2)根据图象直接写出使kx+b<
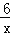 成立的x的取值范围;
成立的x的取值范围;(3)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线的长分别为2和5,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种生物细胞的半径约为0.00028m,将0.00028用科学记数法表示为( )
A.0.28×10﹣3 B.2.8×10﹣4
C.﹣2.8×10﹣5 D.28×10﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个长方体的宽为b(定值),长为x,高为h,体积为V,则V=bxh,其中变量是( )
A. x B. h
C. V D. x,h,V
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=__________时,代数式6x+l与-2x-13的值互为相反数.
相关试题

