【题目】如图,AB是⊙O的直径,C为⊙O上一点,AD平分∠BAC交⊙O于点D,DE∥BC交AC延长线于点E.
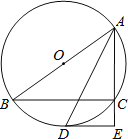
(1)判断DE与⊙O的位置关系并说明理由;
(2)若AB=10,AC=6,求CE的长.
参考答案:
【答案】(1)DE为⊙O的切线;(2)CE=2.
【解析】
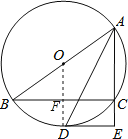
试题分析:(1)连结OD交BC于F,如图,由AD平分∠BAC,得到![]() ,根据垂径定理得到OD⊥BC,根据平行线的性质得到OD⊥DE,即可的结论;
,根据垂径定理得到OD⊥BC,根据平行线的性质得到OD⊥DE,即可的结论;
(2)由圆周角定理得到BC⊥AC,推出四边形ECFD是矩形,求得DF=CE,根据垂径定理得到BF=![]() BC,根据勾股定理得到BC=
BC,根据勾股定理得到BC=![]() =8,OF=
=8,OF=![]() =3,于是得到结论.
=3,于是得到结论.
证明:(1)连结OD交BC于F,如图,
∵AD平分∠BAC,
∴![]() ,
,
∴OD⊥BC,
∵DE∥BC,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∵AB是⊙O的直径,
∴BC⊥AC,
∴四边形ECFD是矩形,
∴DF=CE,
∵OD⊥BC,
∴BF=![]() BC,
BC,
∵BC=![]() =8,
=8,
∴BF=4,
∵OB=![]() AB=5,
AB=5,
∴OF=![]() =3,
=3,
∴DF=2,
∴CE=2.
-
科目: 来源: 题型:
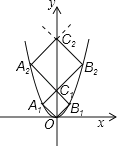
查看答案和解析>>【题目】如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
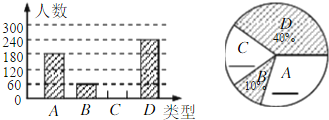
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在AD上,EC平分∠BED.
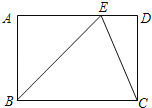
(1)△BEC是否为等腰三角形?为什么?
(2)若AB=a,∠ABE=45°,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】至2010年10月30日上海世博会累计入园人数约7277.99万人,这个数据精确到( )
A. 百分位 B. 百位 C. 千位 D. 万位
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂1月份生产原料a吨,以后每个月比前一个月增产x%,3月份生产原料的吨数是( )
A.a(1+x)2 B.a(1+x%)2 C.a+ax% D.a+a(x%)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售甲、乙两种商品,现有如下信息:

请结合以上信息,解答下列问题:
(1)求甲、乙两种商品的进货单价;
(2)已知甲、乙两种商品的零售单价分别为2元、3元,该商店平均每天卖出甲商品500件和乙商品1300件,经市场调查发现,甲种商品零售单价每降0.1元,甲种商品每天可多销售100件,商店决定把甲种商品的零售单价下降m(m>0)元,在不考虑其他因素的条件下,求当m为何值时,商店每天销售甲、乙两种商品获取的总利润为1800元(注:单件利润=零售单价﹣进货单价)
相关试题

