【题目】已知一副三角板ABE与ACD.
(1)将两个三角板如图(1)放置,连结BD,计算∠1+∠2= .

(2)将图(1)中的三角板BAE绕点A顺时针旋转一个锐角α.
①当α= 时,AB∥CD,如图(2)并计算α+∠1+∠2= .
②当α= 45°时,如图(3),计算α+∠1+∠2= .
③在旋转的过程中,当B点在直线CD的上方时,如图(4), α、∠1、∠2间的数量关系是否会发生变化,为什么?
④当B点运动到直线CD的下方时,如图(5),α(∠CAE)、∠1、∠2间的数量关系是否会发生变化,试说明你的结论?
参考答案:
【答案】 (1)105°;(2)见解析.
【解析】(1)直角三角板一般有两种 ,一种是30°,60°,90° ,另一种是45°,45°,90°.
∴∠BCD=45°+30°=75°
∴∠1+∠2=180°-75°=105°
(2)①连接CE,
若AB∥DC,则∠1+∠2=∠ABE=90°,∴∠BOD=90°
∴∠OCE+∠CEO=180°-∠COE=90°
∴∠ACE+∠AEC=30°+45°+90°=165°
在三角形ACE中,α=180°-165°=15°, α+∠1+∠2=105°
②连接CE
∠EAD+∠ADC=45°+60°=105°, ∴∠DCE+∠AEC=105°
∴∠DCE+∠CEB=105°-45°=60°
∴∠CFE=180°-60°=120°
∴ α+∠1+∠2=180°-120°+45°=105°
③设AC与BE交于点N,BE与CD交于点F
(∠1+∠2)+(∠α+∠C)+∠E=180°,
∠1+∠2+∠α+30°+45°=180°,
∴α+∠1+∠2=105°;
④变化,同上,设AB与DC相交于点F
∠1+(∠α+∠C-∠2)+∠E=180°,
∠1+∠α+30°-∠2+45°=180°,
∴∠α+∠1-∠2=105°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查,比较适用普查而不适用抽样调查方式的是( ).
A.调查全省市场上的“N95口罩”是否符合国家标准;
B.调查一批灯泡的使用寿命;
C.调查你所在班级全体学生的身高;
D.调查我市初中生每人每周的零花钱数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个命题中,错误的命题是( ).
A.四条边都相等的四边形是菱形;
B.对角线互相垂直平分的四边形是正方形;
C.有三个角是直角的四边形是矩形;
D.一组对边平行且相等,对角线垂直且相等的四边形是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算结果为负值的是( )
A.(-7)×(-6)
B.(-6)+(-4)
C.0×(-2) ×(-3)
D.(-7)-(-15) -
科目: 来源: 题型:
查看答案和解析>>【题目】某市2011年全年植树5亿棵,涵养水源3亿立方米.若该市以后每年平均植树5亿棵,到2017年年底“森林城市”的建设将全面完成,那时树木可以长期保持涵养水源11亿立方米.
(1)从2011年到2017年这7年时间里,该市一共要植树多少亿棵?
(2)若把2011年作为第1年,设树木涵养水源的能力y(亿立方米)与第x年成一次函数,求出该函数的表达式,并求出到第5年(即2015年)可以涵养多少水源.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某长途汽车客运公司规定:旅客可随身携带一定质量的行李,若超过规定的质量,则需要购买行李票.已知行李费y(元)是关于x(kg)的一次函数,王先生带60 kg行李需付6元行李费,张先生带80 kg行李需付10元行李费.
(1)求y与x之间的函数表达式.
(2)问:旅客最多可免费携带多少千克行李?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把△ABC平移至A′的位置,使点A与A′对应,得到△A′B′C′;
(2)图中可用字母表示,与线段AA′平行且相等的线段有哪些?
(3)求四边形ACC′A′的面积.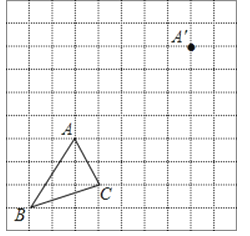
相关试题

