【题目】如图,P是半径为![]() cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
(1)求△PDE的周长;
(2)若DE=![]() cm,求图中阴影部分的面积.
cm,求图中阴影部分的面积.

参考答案:
【答案】(1)6cm;
(2)(4﹣π)cm2 .
【解析】试题分析:(1)根据切线长定理得PA=PB=3cm,CE=BE,AD=DC,由三角形周长定义得△PDE的周长=PE+DE+PD,然后利用等线段可得△PDE的周长=PA+PB=6cm;
(2)连接OB、OA、OE,OD,如图,根据切线的性质得∠OBP=∠OPA=90°,再根据四边形内角和计算出∠BOA=120°,利用切线长定理得BE=CE,DC=DA,则根据三角形面积公式得到S△OCE=S△OBE,S△OCD=S△ODA,所以S五边AOBED=2S△ODE=4,然后根据扇形面积公式和图中阴影部分的面积=S五边AOBED-S扇形AOB进行计算.
试题解析:(1)∵PA、PB、DE是⊙O的切线,
∴PA=PB=3cm,CE=BE,AD=DC,
∴△PDE的周长=PE+DE+PD=PE+CE+CD+PD
=PE+BE+AD+PD
=PA+PB
=3cm+3cm
=6cm;
(2)连接OB、OA、OE,OD,如图,
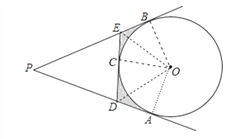
∵PA、PB、OC是⊙O的切线,
∴OB⊥PB,OA⊥PA,OC⊥DE,
∴∠OBP=∠OPA=90°,
∵∠APB=60°,
∴∠BOA=120°,
∵BE=CE,DC=DA,
∴S△OCE=S△OBE,S△OCD=S△ODA ,
∴S五边AOBED=2S△ODE=2×![]() ×
×![]() ×
×![]() =4,
=4,
∴图中阴影部分的面积=S五边AOBED﹣S扇形AOB=4﹣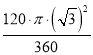 =(4﹣π)cm2.
=(4﹣π)cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2+2a+b2-4b+5=0 ,求ab=_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF.
(1)试说明:△ABC≌△DFE;
(2)若BF=13,EC=7,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将“4排2号”记作(4,2),那么“3排5号”记作 ______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将点A(2,-3)向上平移2个单位后得到的点的坐标为_________.
-
科目: 来源: 题型:
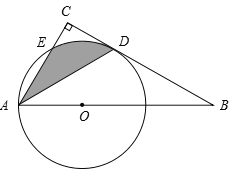
查看答案和解析>>【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC相切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留π
 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》“勾股”章有一题:“今有户高多于广六尺,两隅相去适一丈,问户高、广各几何?”大意是说:已知矩形门的高比宽多6尺,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺),如果设门的宽为x尺,那么这个门的高为(x+6)尺,根据题意得方程:_____.
相关试题

