搜索
【题目】如图，△ABC中，AB=AC，BD=CE，BE=CF，若∠A=50°，则∠DEF的度数是（ ）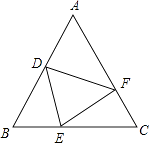 
A.75°
B.70°
C.65°
D.60°
参考答案：
【答案】C
【解析】解：∵AB=AC，
∴∠B=∠C，
在△DBE和△ECF中，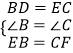
，
∴△DBE≌△ECF（SAS），
∴∠EFC=∠DEB，
∵∠A=50°，
∴∠C=（180°﹣50°）÷2=65°，
∴∠CFE+∠FEC=180°﹣65°=115°，
∴∠DEB+∠FEC=115°，
∴∠DEF=180°﹣115°=65°，
故选：C．
首先证明△DBE≌△ECF，进而得到∠EFC=∠DEB，再根据三角形内角和计算出∠CFE+∠FEC的度数，进而得到∠DEB+∠FEC的度数，然后可算出∠DEF的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在公式s＝s0+vt中，已知s＝100，s0＝25，v＝10，则t＝_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题．
探究一：如图1，在△ABC中，已知O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+
∠A，理由如下：
∵BO和CO分别是∠ABC与∠ACB的平分线，
∴∠1= ∠ABC，∠2= ∠ACB；
∴∠1+∠2= （∠ABC+∠ACB）= （180°﹣∠A）=90°﹣ ∠A，
∴∠BOC=180°﹣（∠1+∠2）=180°﹣（90°﹣ ∠A）=90°+ ∠A．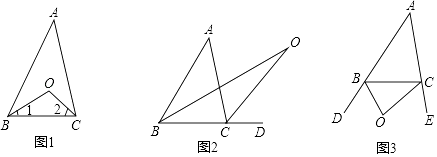
（1）探究二：如图2中，已知O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？并说明理由．
（2）探究二：如图3中，已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？ -
科目： 来源： 题型：
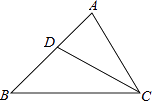
查看答案和解析>>【题目】如图，在△ABC中，CD平分∠ACB，∠A=68°，∠BCD=31°．求∠B，∠ADC的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】3月无锡市商品房平均每平方价格为7500元，7500元用科学记数法表示为元．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，点E在BC上，∠A+∠ADE=180°，∠B=78°，∠C=60°，求∠EDC的度数．
-
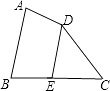
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，D为BC边上一点，∠B=30°，∠DAB=45°．求证：AC=DC．
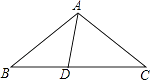
相关试题
