【题目】如图,在△ABC中,CD平分∠ACB,∠A=68°,∠BCD=31°.求∠B,∠ADC的度数. 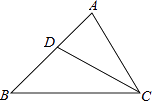
参考答案:
【答案】解:如图,∵CD平分∠ACB,∠BCD=31°,
∴∠ACB=2∠BCD=62°,
又∵∠A=68°,
∴∠B=180°﹣∠A﹣∠ACB=50°,
∴∠ADC=∠B+∠BCD=50°+31°=81°.
综上所述,∠B,∠ADC的度数分别是50°,81°
【解析】由角平分线的性质得到∠ACB=2∠BCD=62°,所以在△ABC中,利用三角形内角和定理来求∠B的度数;利用△BCD外角性质来求∠ADC的度数.
【考点精析】利用三角形的内角和外角和三角形的外角对题目进行判断即可得到答案,需要熟知三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
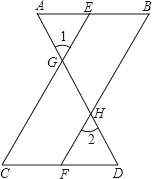
查看答案和解析>>【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD(_______)
∴∠2=∠CGD(等量代换)
∴CE∥BF(_______)
∴∠_____=∠BFD(_______)
又∵∠B=∠C(已知)
∴∠BFD=∠B(等量代换)
∴AB∥CD(_______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在公式s=s0+vt中,已知s=100,s0=25,v=10,则t=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究一:如图1,在△ABC中,已知O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+ ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC与∠ACB的平分线,
∴∠1= ∠ABC,∠2=
∠ABC,∠2=  ∠ACB;
∠ACB;
∴∠1+∠2= (∠ABC+∠ACB)=
(∠ABC+∠ACB)=  (180°﹣∠A)=90°﹣
(180°﹣∠A)=90°﹣  ∠A,
∠A,
∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣ ∠A)=90°+
∠A)=90°+  ∠A.
∠A.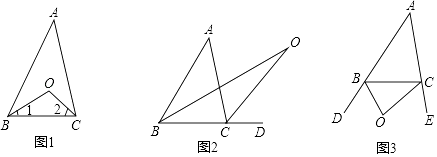
(1)探究二:如图2中,已知O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?并说明理由.
(2)探究二:如图3中,已知O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系? -
科目: 来源: 题型:
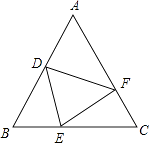
查看答案和解析>>【题目】如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.75°
B.70°
C.65°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】3月无锡市商品房平均每平方价格为7500元,7500元用科学记数法表示为元.
-
科目: 来源: 题型:
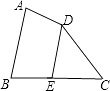
查看答案和解析>>【题目】如图,四边形ABCD中,点E在BC上,∠A+∠ADE=180°,∠B=78°,∠C=60°,求∠EDC的度数.
相关试题

