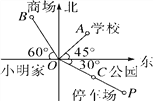
【题目】如图是小明家和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)学校、商场和停车场分别在小明家的什么方位?
(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多远?
参考答案:
【答案】(1)距小明家距离相同的是学校和公园;(2)学校在小明家北偏东45°方向,商场在小明家北偏西30°方向,停车场在小明家南偏东60°方向;(3)停车场距离小明家800m.
【解析】整体分析:
(1)由点A,B,C,P到原点O的距离即可判断;(2)以小明家为中心,计算出学校、商场和停车场的方向角;(3)根据学校距离小明家400m,计算出比例尺即可.
解:(1)∵点C为OP的中点,∴OC=![]() OP=
OP=![]() ×4=2cm.
×4=2cm.
∴OC=OA,
即距小明家距离相同的是学校和公园.
(2)学校在小明家北偏东45°方向,商场在小明家北偏西30°方向,停车场在小明家南偏东60°方向.
(3)图上1cm表示400÷2=200m,
商场距离小明家2.5×200=500m,停车场距离小明家4×200=800m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.

(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积. -
科目: 来源: 题型:
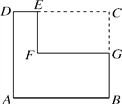
查看答案和解析>>【题目】如图,四边形ABCD是边长为4的正方形,在正方形的一个角上剪去长方形CEFG,其中E,G分别是边CD,BC上的点,且CE=3,CG=2,剩余部分是六边形ABGFED,请你建立适当的直角坐标系求六边形ABGFED各顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一次函数y=
 x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=  x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=  x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由.
相关试题

