【题目】如图,在ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.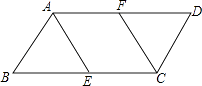
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
参考答案:
【答案】
(1)证明:∵在ABCD中,AB=CD,
∴BC=AD,∠ABC=∠CDA.
又∵BE=EC= ![]() BC,AF=DF=
BC,AF=DF= ![]() AD,
AD,
∴BE=DF.
∴△ABE≌△CDF.
(2)解:∵四边形AECF为菱形,
∴AE=EC.
又∵点E是边BC的中点,
∴BE=EC,即BE=AE.
又BC=2AB=4,
∴AB= ![]() BC=BE,
BC=BE,
∴AB=BE=AE,即△ABE为等边三角形,
ABCD的BC边上的高为2×sin60°= ![]() ,
,
∴菱形AECF的面积为2 ![]() .
.
【解析】(1)在ABCD中,AB=CD,得到BC=AD,∠ABC=∠CDA,又因为BE=EC= BC÷2,AF=DF= AD÷2,得到BE=DF,得到△ABE≌△CDF;(2)由四边形AECF为菱形,得到AE=EC,得到AE=EC,又点E是边BC的中点,得到BE=EC,即BE=AE,又BC=2AB=4,得到AB=BE,得到AB=BE=AE,即△ABE为等边三角形,所以ABCD的BC边上的高为2×sin60°=![]() ,菱形AECF的面积为2
,菱形AECF的面积为2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,乙出发,设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h),y甲、y乙与x之间的函数图象如图所示.
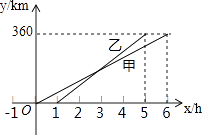
(1)甲的速度是km/h;
(2)当1≤x≤5时,求y乙关于x的函数解析式;
(3)当乙与A地相距240km时,甲与A地相距km. -
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法将2.896精确到0.01,所得到的近似数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个x的值说明“|x|=x”是错误的,这个值可以是x=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大黄鱼是中国特有的地方性鱼类,有“国鱼”之称,由于过去滥捕等多种因素,大黄鱼资源已基本枯竭,目前,我市已培育出十余种大黄鱼品种,某鱼苗人工养殖基地对其中的四个品种“宁港”、“御龙”、“甬岱”、“象山港”共300尾鱼苗进行成活实验,从中选出成活率最高的品种进行推广,通过实验得知“甬岱”品种鱼苗成活率为
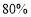 ,并把实验数据绘制成下列两幅统计图(部分信息未给出):
,并把实验数据绘制成下列两幅统计图(部分信息未给出):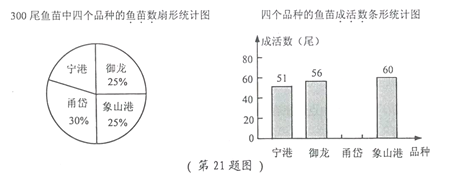
(1) 求实验中“宁港”品种鱼苗的数量;
(2) 求实验中“甬岱”品种鱼苗的成活数,并补全条形统计图;
(3)你认为应选哪一品种进行推广?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
如图,将矩形
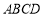 的四边
的四边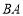 、
、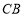 、
、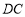 、
、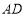 分别延长至
分别延长至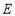 、
、 、
、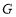 、
、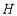 ,使得
,使得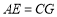 ,
,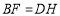 ,连接
,连接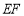 ,
,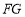 ,
,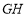 ,
,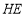 .
.(1) 求证:四边形
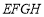 为平行四边形;
为平行四边形;(2) 若矩形
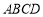 是边长为1的正方形,且
是边长为1的正方形,且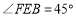 ,
,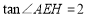 ,求
,求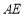 的长.
的长.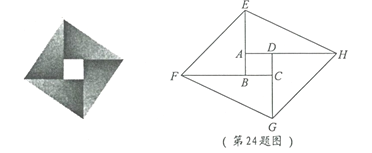
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是720°,这个多边形的边数是( )
A.4
B.5
C.6
D.7
相关试题

