【题目】如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE , AD与BE相交于点F . 
(1)试说明△ABD≌△BCE;
(2)△EAF与△EBA相似吗?说说你的理由.
参考答案:
【答案】
(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABD=∠BCE=∠BAC,
又∵BD=CE,
∴△ABD≌△BCE;
(2)解:相似;
理由如下:
∵△ABD≌△BCE,
∴∠BAD=∠CBE,
∴∠BAC-∠BAD=∠CBA-∠CBE,
∴∠EAF=∠EBA,又∵∠AEF=∠BEA,
∴△EAF∽△EBA.
【解析】(1)根据等边三角形各边长相等和各内角为60°的性质可以求证△ABD≌△BCE;(2)根据全等三角形对应角相等性质可得∠BAD=∠CBE , 进而可以求得∠EAF=∠EBA , 即可求证△EAF∽△EBA , 即可解题.
【考点精析】认真审题,首先需要了解相似三角形的判定(相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是直角三角形ABC斜边上的中线,AE⊥AD交CB延长线于E , 则图中一定相似的三角形是( )

A.△AED与△ACB
B.△AEB与△ACD
C.△BAE与△ACE
D.△AEC与△DAC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是直角△ABC (∠C=90°)的角平分线,EF⊥AD于D , 与AB及AC的延长线分别交于E , F , 写出图中的一对全等三角形是 ;一对相似三角形是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在Rt△ABC中∠C=90°,CD为AB边上的高. 求证:Rt△ADC∽Rt△CDB .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )
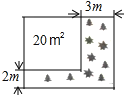
A.7m
B.8m
C.9m
D.10m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( )
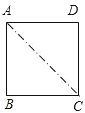

A.0.5cm
B.1cm
C.1.5cm
D.2cm -
科目: 来源: 题型:
查看答案和解析>>【题目】学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为

相关试题

