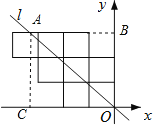
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )

A.y=﹣x B.y=﹣![]() x C.y=﹣
x C.y=﹣![]() x D.y=﹣
x D.y=﹣![]() x
x
参考答案:
【答案】D
【解析】
试题分析:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标即可得到该直线l的解析式.
解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴S△AOB=4+1=5,
∴![]() OBAB=5,
OBAB=5,
∴AB=![]() ,
,
∴OC=![]() ,
,
由此可知直线l经过(﹣![]() ,3),
,3),
设直线方程为y=kx,
则3=﹣![]() k,
k,
k=﹣![]() ,
,
∴直线l解析式为y=﹣![]() x,
x,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微小的无花果,质量只有0.000000076克,将数0.000000076用科学记数法表示为( )
A.7.6×10﹣9 B.7.6×10﹣8 C.7.6×109 D.7.6×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线互相垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
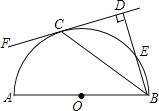
(1)求证:CD是半圆O的切线.
(2)若DC=8,BE=4,求圆的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在环境创优活动中,某居民小区要在一块靠墙(墙长25米)的空地上修建一个矩形养鸡场,养鸡场的一边靠墙,如果用60m长的篱笆围成中间有一道篱笆的养鸡场,设养鸡场平行于墙的一边BC的长为x(m),养鸡场的面积为y(m2)
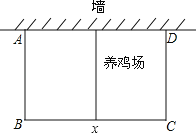
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)养鸡场的面积能达到300m2吗?若能,求出此时x的值,若不能,说明理由;
(3)根据(1)中求得的函数关系式,判断当x取何值时,养鸡场的面积最大?最大面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面计算正确的是( )
A. ﹣5×(﹣4)×(﹣2)×(﹣2)=5×4×2×2=80
B. 12×(﹣5)=﹣50
C. (﹣9)×5×(﹣4)×0=9×5×4=180
D. (﹣36)×(﹣1)=﹣36
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中正确的有几个( )
①关于一条直线对称的两个图形一定能重合;
②两个能重合的图形一定关于某条直线对称;
③两个轴对称图形的对应点一定在对称轴的两侧.;
④角平分线是角的对称轴.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
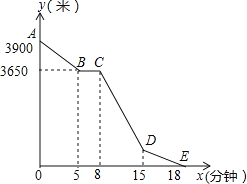
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
相关试题

