搜索
【题目】一组数据5，﹣2，3，x，3，﹣2，若每个数据都是这组数据的众数，则这组数据的平均数是 ．
参考答案：
【答案】2
【解析】解：若每个数据都是这组数据的众数，则x=5，
所以这组数据的平均数是12÷6=2．
所以答案是：2．
【考点精析】掌握算术平均数和中位数、众数是解答本题的根本，需要知道总数量÷总份数=平均数．解题关键是根据已知条件确定总数量以及与它相对应的总份数；中位数是唯一的，仅与数据的排列位置有关，它不能充分利用所有数据；众数可能一个，也可能多个，它一定是这组数据中的数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若m、n是一元二次方程x2﹣5x﹣2=0的两个实数根，则m+n﹣mn的值是（ ）
A.﹣7
B.7
C.3
D.﹣3 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为2的等边△ABC中，AD⊥BC，点P为边AB 上一个动点，过点P作PF∥AC交线段BD于点F，作PG⊥AB交AD于点E，交线段CD于点G，设
， 
．（1）求证：
；（2）求y关于x的函数解析式，并写出x的取值范围；
（3）以P、E、F为顶点的三角形与△EDG能否相似？如果能相似，请求出.BP的长，如果不能，请说明理由．
（备用图）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P为AD的中点，连接AE、BD．
（1）猜想PM与PN的数量关系及位置关系，请直接写出结论；
（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP、BD分别交于点G、H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；
（3）若图②中的等腰直角三角形变成直角三角形，使BC=kAC，CD=kCE，如图③，写出PM与PN的数量关系，并加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某电视台为了解本地区电视节目的收视情况，对部分广州开展了“你最喜爱的电视节目”的问卷调查（每人只填写一项），根据收集的数据绘制了下面两幅不完整的统计图，根据要求回答下列问题：
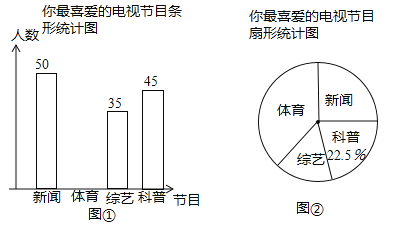
（1）本次问卷调查共调查了 名观众；
（2）图②中最喜爱“新闻节目”的人数占调查总人数的百分比为 ，“综艺节目”在扇形统计图中所对应的圆心角的度数为 ；
（3）补全图①中的条形统计图；
（4）现有最喜爱“新闻节目”（记为
），“体育节目”（记为
），“综艺节目”（记为C），“科普节目”（记为D）的观众各一名，电视台要从四人中随机抽取两人参加联谊活动，请用列表或画树状图的方法，求出恰好抽到最喜爱“B”和“C”两位观众的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】一个多边形的每个内角都等于144°，那么这个多边形的内角和为（ ）
A. 1980°B. 1800°C. 1620°D. 1440°
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们规定:满足(1)各边互不相等且均为整数;(2)最短边上的高与最长边上的高的比值为整数k,这样的三角形称为“比高三角形”,其中k叫做“比高系数”.那么周长为13的三角形的“比高系数”k=____.
相关试题
