【题目】如图1,BC是⊙O的直径,点A在⊙O上,点D在CA的延长线上,DE⊥BC,垂足为点E,DE与⊙O相交于点H,与AB相交于点l,过点A作⊙O的切线AF,与DE相交于点F.
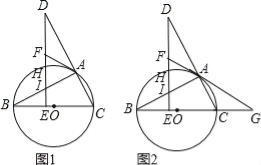
(1)求证:∠DAF=∠ABO;
(2)当AB=AD时,求证:BC=2AF;
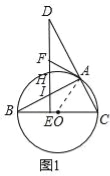
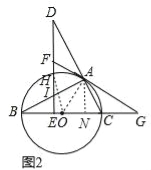
(3)如图2,在(2)的条件下,延长FA,BC相交于点G,若tan∠DAF=![]() ,EH=2
,EH=2![]() ,求线段CG的长.
,求线段CG的长.
参考答案:
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
试题分析:(1)连接AO,如图1,由OA=OB可得∠OAB=∠OBA,要证∠DAF=∠ABO,只需证∠DAF=∠BAO,只需证∠FAO=∠DAB=90°即可;
(2)由于BC=2OA,要证BC=2AF,只需证OA=AF,只需证△AFD≌△AOB即可;
(3)过点A作AN⊥BC于N,连接OH,OA,如图2,易得BE=2IE,DE=2EC,DI=2AF=BC,从而可得EC=3IE=![]() BE.设BE=2x,则有EC=3x,BC=5x,HO=BO=
BE.设BE=2x,则有EC=3x,BC=5x,HO=BO=![]() ,EO=
,EO=![]() .在Rt△HEO中运用勾股定理可求出x.利用三角函数可得BN=2AN=4NC,则有BC=5NC=10,从而可求出NC、ON,易证△AON∽△GOA,根据相似三角形的性质可求出OG,从而可求出CG.
.在Rt△HEO中运用勾股定理可求出x.利用三角函数可得BN=2AN=4NC,则有BC=5NC=10,从而可求出NC、ON,易证△AON∽△GOA,根据相似三角形的性质可求出OG,从而可求出CG.
试题解析:(1)连接AO,如图1.
∵AF与⊙O相切于点A,
∴OA⊥AF,即∠FAO=90°.
∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠DAB=90°,
∴∠FAO=∠DAB=90°,
∴∠DAF=∠BAO.
∵OA=OB,
∴∠OAB=∠OBA,
∴∠DAF=∠ABO;
(2)∵DE⊥BC,∴∠DEB=90°,
∴∠DIB=90°+∠ABO.
∵∠DIB=90°+∠D,
∴∠D=∠ABO.
在△AFD和△AOB中,
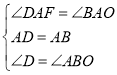 ,
,
∴△AFD≌△AOB,
∴AF=AO,
∴BC=2OA=2AF;
(3)过点A作AN⊥BC于N,连接OH,OA,如图2.
∵∠D=∠B=∠BAO=∠DAF,tan∠DAF=![]() ,
,
∴tanB=![]() ,tanD=
,tanD=![]() ,
,
∴BE=2IE,DE=2EC.
又∵∠DIA+∠D=∠DAF+∠FAI=90°,
∴∠FIA=∠FAI,
∴FI=FA,
∴DI=2AF=BC,
∴DE﹣IE=BE+EC,
∴2EC﹣IE=2IE+EC,
∴EC=3IE=![]() BE.
BE.
设BE=2x,则有EC=3x,BC=5x,HO=BO=![]() ,EO=
,EO=![]() .
.
在Rt△HEO中,根据勾股定理可得
(![]() )2+(2
)2+(2![]() )2=(
)2=(![]() )2,
)2,
解得x=2(舍负).
∵AN⊥BC,∠BAC=90°,
∴∠NAC=∠ABC,
∴tan∠NAC=![]() ,tan∠ABC=
,tan∠ABC=![]() ,
,
∴BN=2AN=4NC,
∴BC=5NC=10,
∴NC=2,ON=5﹣2=3.
∵∠AON=∠GOA,∠ANO=∠OAG=90°,
∴△AON∽△GOA,
∴![]() ,
,
∴![]() ,
,
∴OG=![]() ,
,
∴CG=OG﹣OC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一边为6,另一边为12,则其周长为.
-
科目: 来源: 题型:
查看答案和解析>>【题目】书包里放有语文、数学、英语、生物、历史5本教科书,从中任意抽取2本,则抽取的2本中其中一本是数学教科书的情况有( )种.
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自然保护区的面积为2150 000 000平方米,2150000000这个数用科学计数法表示为:
A. 2.15×108 B. 21.5×108 C. 2.15×109 D. 0.215×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,是一张直角三角形的纸片,两直角边AC=6㎝,BC=8㎝,现将△ABC折叠,使点B与点A重合,折痕为DE,则AD的长为( )
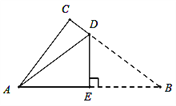
A. 4㎝ B. 5㎝ C. 6㎝ D.
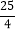 ㎝
㎝ -
科目: 来源: 题型:
查看答案和解析>>【题目】方程2 014x-m=2 015的解是x=1,则m=_______.
相关试题

