【题目】如图,E、F分别是AD和BC上的两点,EF将四边形ABCD分成两个边长为5cm的正方形,∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm,点P从点H出发,沿HD以lcm/s的速度运动,同时点Q从点A出发,沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.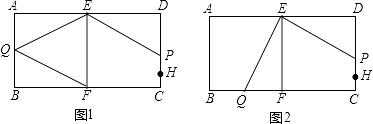
(1)用t表示△EPD的面积;
(2)试探究:当t为何值时,△EPD的面积等于△EQF面积的 ![]() ?
?
参考答案:
【答案】
(1)(10﹣2.5t)cm2
(2)
解:分三种情况讨论:
①如图1所示,过Q作QM⊥EF,垂足为M.

∵四边形ABFE是正方形,
∴QM=AE=5cm.
当0<t≤1时,S△EQF= ![]() EF×QM=
EF×QM= ![]() ×5×5=12.5,S△EPD=
×5×5=12.5,S△EPD= ![]() ED×DP=
ED×DP= ![]() ×5×(4﹣t)=10﹣2.5t,
×5×(4﹣t)=10﹣2.5t,
当 ![]() S△EQF=S△EPD时,即
S△EQF=S△EPD时,即 ![]() ×12.5=10﹣2.5t,
×12.5=10﹣2.5t,
解得,t=0.5;
②当1<t≤2时,S△EQF= ![]() ×EF×FQ=2.5FQ,S△EPD=
×EF×FQ=2.5FQ,S△EPD= ![]() ED×DP=
ED×DP= ![]() ×5×(4﹣t)=10﹣2.5t,
×5×(4﹣t)=10﹣2.5t,

∵FQ=10﹣5t,
∴ ![]() ×2.5(10﹣5t)=10﹣2.5t,
×2.5(10﹣5t)=10﹣2.5t,
解得:t=1.2;
③当2<t≤3时,S△EQF= ![]() FQ×EF=2.5(5t﹣10),S△EPD=
FQ×EF=2.5(5t﹣10),S△EPD= ![]() ED×DP=
ED×DP= ![]() ×5×(4﹣t)=10﹣2.5t,
×5×(4﹣t)=10﹣2.5t,

∴ ![]() ×2.5×(5t﹣10)=2.5(4﹣t),
×2.5×(5t﹣10)=2.5(4﹣t),
解得:t= ![]() ;
;
综上所述:当t的值为0.5s或1.2s或 ![]() s时,△EPD的面积等于△EQF面积的
s时,△EPD的面积等于△EQF面积的 ![]() .
.
【解析】解:(1)S△EPD= ![]() ED×DP=
ED×DP= ![]() ×5×(4﹣t)=10﹣2.5t;所以答案是:(10﹣2.5t)cm2;
×5×(4﹣t)=10﹣2.5t;所以答案是:(10﹣2.5t)cm2;
【考点精析】通过灵活运用三角形的面积,掌握三角形的面积=1/2×底×高即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程
(1)
(2) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①35=3×3×3×3×3;②﹣1是单项式,且它的次数为1;③若∠1=90°﹣∠2,则∠1与∠2互为余角;④对于有理数n、x、y(其中xy≠0),若
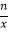 =
= 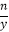 ,则x=y.其中不正确的有( )
,则x=y.其中不正确的有( )
A.3个
B.2个
C.1个
D.0个 -
科目: 来源: 题型:
查看答案和解析>>【题目】点P(a-2,3a+6)到两条坐标轴的距离相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,若∠DBE=78°,则∠A+∠C+∠D+∠E=°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子正确的是( )
A.若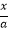 <
<  ,则x<y
,则x<y
B.若bx>by,则x>y
C.若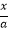 =
=  ,则x=y
,则x=y
D.若mx=my,则x=y
相关试题

