【题目】如图,已知二次函数的图象经过点A(3,3)、B(4,0)和原点O.P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
(1)求直线OA和二次函数的解析式;
(2)当点P在直线OA的上方时,
①当PC的长最大时,求点P的坐标;
②当S△PCO=S△CDO时,求点P的坐标.


参考答案:
【答案】(1)y=x,y=﹣x2+4x;(2)①P(![]() ,
, ![]() );②P(2,4).
);②P(2,4).
【解析】试题分析: ![]() 设
设![]() 把A点坐标代入即可求出二次函数解析式.设出直线
把A点坐标代入即可求出二次函数解析式.设出直线![]() 的解析式,把点
的解析式,把点![]() 坐标代入即可.
坐标代入即可.
![]() ①根据点的坐标求出
①根据点的坐标求出![]() 化成顶点式即可求出线段
化成顶点式即可求出线段![]() 的最大值;
的最大值;
②根据点的坐标设出点P和点C的坐标,表示出PC和CD的长度,要使得![]() 则有
则有![]() 代入求出坐标即可;
代入求出坐标即可;
试题解析: ![]() 设
设![]()
把A点坐标![]() 代入得:
代入得:![]()
故函数的解析式为![]()
设直线OA的解析式为![]() 把
把![]() 入得:
入得: ![]()
∴直线OA的解析式为![]()
![]()
![]()
![]() 轴,P在
轴,P在![]() 上,C在
上,C在![]() 上,
上,
![]()
![]()
①![]()
∴当![]() 时,PC的长最大,
时,PC的长最大,
![]()
②当![]() 时,即
时,即![]()
当![]() 时,则有
时,则有![]() 解得
解得![]() (舍去),
(舍去),
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九(1)班学生参加毕业体考的成绩统计如图所示,请根据统计图中提供的信息完成后面的填空题(将答案填写在相应的横线上)
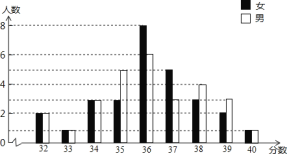
(1)该班共有______名学生;
(2)该班学生体考成绩的众数是______;男生体考成绩的中位数是______;
(3)若女生体考成绩在37分及其以上,男生体考成绩在38分及其以上被认定为体尖生,则该班共有_______名体尖生.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)乙车休息了 _________ h;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)到目前为止,已研究的图形变换有哪几种?这些变换的共同性质有哪些?
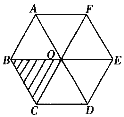
(2)如图,O是正六边形ABCDEF的中心,图中可由△OBC旋转得到的三角形有a个,可由△OBC平移得到的三角形有b个,可由△OBC轴对称得到的三角形有c个,试求(a+b+c)a+b-c的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B'点,AE是折痕。

(1)试判断B'E与DC的位置关系并说明理由。
(2)如果∠C=130°,求∠AEB的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与反比例函数
的图象与反比例函数 在第一象限的图象交于
在第一象限的图象交于 和B两点,与x轴交于点C.
和B两点,与x轴交于点C.(1)求反比例函数的解析式及点C的坐标.
(2)求△OCA的面积

相关试题

