【题目】2018雾霾天气趋于严重,某商场根据民众健康需要,从厂家购进了A,B两种型号的空气净化器,如果销售15台A型和10台B型空气净化器的利润为6000元,销售10台A型和15台B型空气净化器的利润为6500元.
(1)求每台A型空气净化器和B型空气净化器的销售利润;
(2)该商场计划一次购进两种型号的空气净化器共160台,其中B型空气净化器的进货量不超过A型空气净化器的2倍,设购进A型空气净化器x台,这160台空气净化器的销售总利润为y元.
①求y关于x的函数关系式;
②该公司购进A型、B型空气净化器各多少台时,才能使销售总利润最大?
参考答案:
【答案】(1) 每台A型空气净化器得销售利润为200元,每台B型空气净化器的销售利润为300元;(2)①y=100x+48000;②该公司购进A型、B型空气净化器分别为54台、106台时,才能使销售总利润最大.
【解析】
(1)根据题意可以列出相应的二元一次方程组,从而可以解答本题;
(2)①根据题意可以得到y与x的函数关系式;
②根据题意可以求得x的取值范围,由①中的函数关系,从而可以得到该公司购进A型、B型空气净化器各多少台时,才能使销售总利润最大.
(1)设每台A型空气净化器得销售利润为a元,每台B型空气净化器的销售利润为b元,
![]() ,得
,得![]() ,
,
即每台A型空气净化器得销售利润为200元,每台B型空气净化器的销售利润为300元;
(2)①由题意可得,y=200x+(160x)×300=100x+48000,
即y关于x的函数关系式是y=100x+48000;
②由题意可得,
160x2x,得![]() ,
,
∵y=100x+48000,
∴x=54时,y取得最大值,此时,160x=106,
即该公司购进A型、B型空气净化器分别为54台、106台时,才能使销售总利润最大.
-
科目: 来源: 题型:
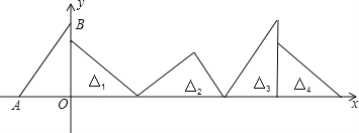
查看答案和解析>>【题目】 如图,在直角坐标系中,已知点A(-3,0),B(0,4),AB=5,对△OAB连续做旋转变换,依次得到△1,△2,△3,△4,…,则△2017的直角顶点的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
-
科目: 来源: 题型:
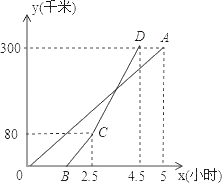
查看答案和解析>>【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
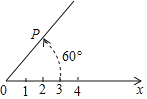
A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:
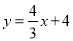 分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2:
分别与x轴、y轴交于A、B两点,点C为x轴上任意一点,直线l2: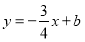 经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.
经过点C,且与直线l1交于点D,与y轴交于点E,连结AE.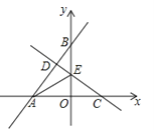
(1)当点C的坐标为
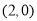 时,①求直线l2的函数表达式;②求证:AE平分
时,①求直线l2的函数表达式;②求证:AE平分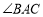 ;
;(2)问:是否存在点C,使
 是以CE为一腰的等腰三角形?若存在,直接写出点C的坐标;若不存在,请说明理由.
是以CE为一腰的等腰三角形?若存在,直接写出点C的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
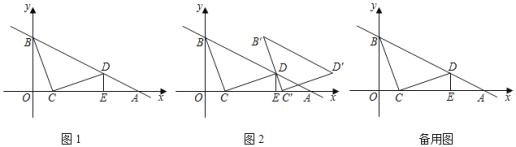
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线y=-
 x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;
(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
相关试题

