【题目】如图,在等边△ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F.
(1)求证:AD=CE;
(2)求∠DFC的度数.

参考答案:
【答案】(1)证明详见解析;(2)60°.
【解析】
试题分析:根据等边三角形的性质,利用SAS证得△AEC≌△BDA,所以AD=CE,∠ACE=∠BAD,再根据三角形的外角与内角的关系得到∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
试题解析:(1)∵△ABC是等边三角形,
∴∠BAC=∠B=60°,AB=AC.
又∵AE=BD,
∴△AEC≌△BDA(SAS).
∴AD=CE;
(2)∵(1)△AEC≌△BDA,
∴∠ACE=∠BAD,
∴∠DFC=∠FAC+∠ACF=∠FAC+∠BAD=∠BAC=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3xm+5y2与-2x3yn是同类项,则m-2n=______
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A. 三点确定一个圆 B. 三角形有且只有一个外接圆
C. 四边形都有一个外接圆 D. 圆有且只有一个内接三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在9×7的小正方形网格中,△ABC的顶点A,B,C在网格的格点上.将△ABC向左平移3个单位、再向上平移3个单位得到△A′B′C′.再将△ABC按一定规律依次旋转:第1次,将△ABC绕点B顺时针旋转
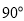 得到△
得到△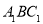 ;第2次,将△
;第2次,将△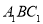 绕点
绕点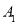 顺时针旋转
顺时针旋转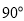 得到△
得到△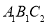 ;第3次,将△
;第3次,将△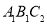 绕点
绕点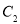 顺时针旋转
顺时针旋转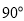 得到△
得到△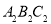 ;第4次,将△
;第4次,将△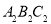 绕点
绕点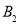 顺时针旋转
顺时针旋转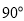 得到△
得到△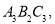 依次旋转下去.
依次旋转下去.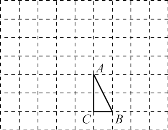
(1)在网格中画出△A′B′C′和△
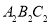 ;
;(2)请直接写出至少在第几次旋转后所得的三角形刚好为△A′B′C′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,分别以△ABC的三边为边在BC的同侧作正△BCE、正△ABF和正△ACD,已知BC=3,高AH=1,则五边形BCDEF的面积是( )
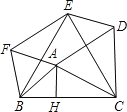
A.
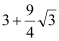 B.
B.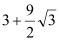 C.6 D.
C.6 D.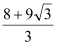
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2a2+4a+2=___________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+k=0的一个根是3,则另一个根是__.
相关试题

