【题目】如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上. 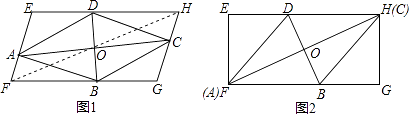
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知 ![]() =2,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
=2,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
参考答案:
【答案】
(1)证明:∵点O是菱形ABCD对角线AC、BD的交点,
∴OA=OC,OD=OB,
∵点O是线段FH的中点,
∴OF=OH.
在△AOF和△COH中,有  ,
,
∴△AOF≌△COH(SAS),
∴∠AFO=∠CHO,
∴AF∥CH.
同理可得:DH∥BF.
∴四边形EFGH是平行四边形
(2)设矩形EFGH的长为a、宽为b,则AC= ![]() .
.
∵ ![]() =2,
=2,
∴BD= ![]() AC=
AC= ![]() ,OB=
,OB= ![]() BD=
BD= ![]() ,OA=
,OA= ![]() AC=
AC= ![]() .
.
∵四边形ABCD为菱形,
∴AC⊥BD,
∴∠AOB=90°.
∵四边形EFGH是矩形,
∴∠AGH=90°,
∴∠AOB=∠AGH=90°,
又∵∠BAO=∠CAG,
∴△BAO∽△CAG,
∴ ![]() ,即
,即 ![]() ,
,
解得:a=2b①.
∵S菱形ABCD= ![]() ACBD=
ACBD= ![]()
![]()
![]() =20,
=20,
∴a2+b2=80②.
联立①②得: ![]() ,
,
解得: ![]() ,或
,或 ![]() (舍去).
(舍去).
∴矩形EFGH的长为8,宽为4
【解析】(1)根据菱形的性质可得出OA=OC,OD=OB,再由中点的性质可得出OF=OH,结合对顶角相等即可利用全等三角形的判定定理(SAS)证出△AOF≌△COH,从而得出AF∥CH,同理可得出DH∥BF,依据平行四边形的判定定理即可证出结论;(2)设矩形EFGH的长为a、宽为b.根据勾股定理及边之间的关系可找出AC= ![]() ,BD=
,BD= ![]() ,利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°,从而可证出△BAO∽△CAG,根据相似三角形的性质可得出
,利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°,从而可证出△BAO∽△CAG,根据相似三角形的性质可得出 ![]() ,套入数据即可得出a=2b①,再根据菱形的面积公式得出a2+b2=80②,联立①②解方程组即可得出结论.本题考查了平行四边形的判定、全等三角形的判定及性质、菱形的性质、矩形的性质以及相似三角形的判定及性质,解题的关键:(1)找出AF∥CH、DH∥BF;(2)找出关于a、b的二元二次方程组.本题属于中档题,难度不大,但解题过程叫繁琐,解决该题型题目时,根据相似三角形的性质找出对应边的比例关系是关键.
,套入数据即可得出a=2b①,再根据菱形的面积公式得出a2+b2=80②,联立①②解方程组即可得出结论.本题考查了平行四边形的判定、全等三角形的判定及性质、菱形的性质、矩形的性质以及相似三角形的判定及性质,解题的关键:(1)找出AF∥CH、DH∥BF;(2)找出关于a、b的二元二次方程组.本题属于中档题,难度不大,但解题过程叫繁琐,解决该题型题目时,根据相似三角形的性质找出对应边的比例关系是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
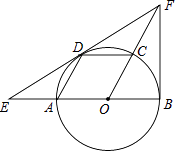
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】蔬菜经营户老王,近两天经营的是青菜和西兰花.
(1)昨天的青菜和西兰花的进价和售价如表,老王用600元批发青菜和西兰花共200市斤,当天售完后老王一共能赚多少元钱?青菜
西兰花
进价(元/市斤)
2.8
3.2
售价(元/市斤)
4
4.5
(2)今天因进价不变,老王仍用600元批发青菜和西兰花共200市斤.但在运输中青菜损坏了10%,而西兰花没有损坏仍按昨天的售价销售,要想当天售完后所赚的钱不少于昨天所赚的钱,请你帮老王计算,应怎样给青菜定售价?(精确到0.1元) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
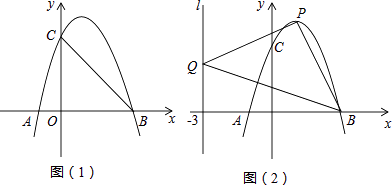
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( )

A.5
B.7
C.9
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】三张背面完全相同的数字牌,它们的正面分别印有数字“1”、“2”、“3”,将它们背面朝上,洗匀后随机抽取一张,记录牌上的数字并把牌放回,再重复这样的步骤两次,得到三个数字a、b、c,则以a、b、c为边长正好构成等边三角形的概率是( )
A.
B.
C.
D.
相关试题

