【题目】如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:![]() ≈1.73,
≈1.73,![]() ≈1.41.
≈1.41.

参考答案:
【答案】约是5.3米.
【解析】试题分析:由条件可知BE=DE=20米,再在Rt△BCE中,利用三角函数可求得BC的长,进而可求得AB的长.
试题解析:∵∠BEC=∠BDE+∠DBE,∴∠DBE=∠BEC-∠BDC=60°-30°=30°,∴∠BDE=∠DBE,∴BE=DE=20米.在Rt△BCE中,∠BCE=90°,sin∠BEC=![]() ,∴
,∴![]() (米),∴AB=BC-AC=17.3-12=5.3(米).答:旗杆AB的高度为5.3米.
(米),∴AB=BC-AC=17.3-12=5.3(米).答:旗杆AB的高度为5.3米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是 ( )
A. 三角形的角平分线是一条射线.B. 三角形的一个外角大于任何一个内角.
C. 任意三角形的外角和都是180°.D. 内角和是1080°的多边形是八边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AE是中线,AD是角平分线,AF是高,∠B=30°,∠C=80°,BE=3,AF=2,填空:
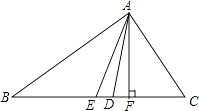
(1)AB=;
(2)∠BAD=;
(3)∠DAF=;
(4)S△AEC= . -
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列已知条件,能够画出唯一△ABC的是( )
A. AB=5,BC=6,∠A=70° B. AB=5,BC=6,AC=13
C. ∠A=50°,∠B=80°,AB=8 D. ∠A=40°,∠B=50°,∠C=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每一个外角都等于40°,则这个多边形的边数是 .
-
科目: 来源: 题型:
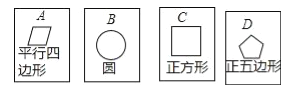
查看答案和解析>>【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=400 ,当∠C=____时,△ABC为等腰三角形.
相关试题

