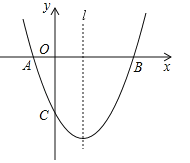
【题目】如图,已知抛物线![]() (a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
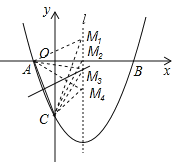
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
参考答案:
【答案】(1)![]() ;(2)P(1,0);(3).
;(2)P(1,0);(3).
【解析】
试题分析:(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可;
(2)由图知:A.B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l与x轴的交点,即为符合条件的P点;
(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、③AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
试题解析:(1)将A(﹣1,0)、B(3,0)、C(0,﹣3)代入抛物线![]() 中,得:
中,得: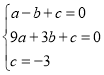
,解得: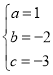 ,故抛物线的解析式:
,故抛物线的解析式:![]() .
.
(2)当P点在x轴上,P,A,B三点在一条直线上时,点P到点A、点B的距离之和最短,此时x=![]() =1,故P(1,0);
=1,故P(1,0);
(3)如图所示:抛物线的对称轴为:x=![]() =1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
=1,设M(1,m),已知A(﹣1,0)、C(0,﹣3),则:
![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =10;
=10;
①若MA=MC,则![]() ,得:
,得:![]() =
=![]() ,解得:m=﹣1;
,解得:m=﹣1;
②若MA=AC,则![]() ,得:
,得:![]() =10,得:m=
=10,得:m=![]() ;
;
③若MC=AC,则![]() ,得:
,得:![]() =10,得:
=10,得:![]() ,
,![]() ;
;
当m=﹣6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,![]() )(1,
)(1,![]() )(1,﹣1)(1,0).
)(1,﹣1)(1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】有A、B、C、D四位员工做一项工作,每天必须是三位员工同时做,另一位员工休息,当完成这项工作时,D做了8天,比其他任何人都多,B做了5天,比其他任何人都少,那么A做了_____天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.(1)求二次函数
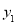 的解析式;
的解析式;(2)将
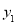 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线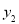 ,直线y=m(m>0)交
,直线y=m(m>0)交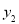 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);(3)在(2)的条件下,
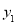 、
、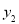 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与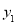 、
、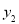 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与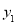 、
、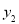 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.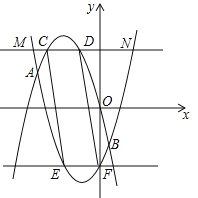
-
科目: 来源: 题型:
查看答案和解析>>【题目】用不等式表示“x与5的差不小于4”:.
-
科目: 来源: 题型:
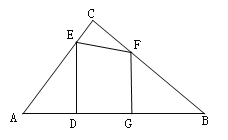
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90,AB=10,AC=6,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
(1)当AD=3时,求DE的长;
(2)当点E、F在边AC、BC上移动时,设
 ,
,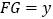 ,
,求
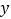 关于
关于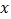 的函数解析式。
的函数解析式。(3)在点E、F移动过程中,△AED与△CEF能否相似,若能,求AD的长;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年,合肥市户籍人口数约为801.4万人,将801.4万用科学记数法表示应是 .
相关试题

