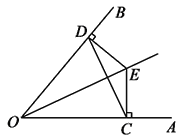
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
(1)求证:ED=EC;
(2)求证:∠ECD=∠EDC;
(3)求证:OE垂直平分CD.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)根据角平分线的性质进行判断;
(2)根据等边对等角即可得出结论;
(3)先判定Rt△OCE≌Rt△ODE(HL),得出OC=OD,进而得到点O在CD的垂直平分线上,再根据EC=DE,可得点E在CD的垂直平分线上,进而得到OE是CD的垂直平分线.
证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴ED=EC;
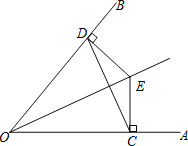
(2)∵EC=DE,
∴∠ECD=∠EDC;
(3)在Rt△OCE和Rt△ODE中,
![]() ,
,
∴Rt△OCE≌Rt△ODE(HL),
∴OC=OD,
∴点O在CD的垂直平分线上,
又∵EC=DE,
∴点E在CD的垂直平分线上,
∴OE垂直平分CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级共有8个班,241名同学,历史老师为了了解新中考模式下该校八年级学生选修历史学科的意向,请小红,小亮,小军三位同学分别进行抽样调查.三位同学调查结果反馈如下:

小红、小亮和小军三人中,你认为哪位同学的调查结果较好地反映了该校八年级同学选修历史的意向,请说出理由,并由此估计全年级有意向选修历史的同学的人数. -
科目: 来源: 题型:
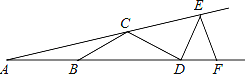
查看答案和解析>>【题目】如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.

(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】寿春诵读会让寿春师生成为最美的“朗读者”,极大地激发了学生的阅读兴趣.学校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了名学生;
(2)将表示“生活类”的条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是BC的中点,DE垂直平分AC,垂足为E,F是BA的中点.求证:DF是AB的垂直平分线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O是AB上的一点,从O点引出射线OC、OE、OD,其中OE平分∠BOC.
(1)如图1,若∠COD是直角,∠DOE=15°,求∠AOE的度数;
(2)如图1,若∠AOC=∠BOD,∠DOE=15°,求∠AOE的度数;
(3)将图1中的∠COD (∠COD仍是直角)绕顶点O顺时针旋转至图2的位置,若∠AOC=
 , ∠DOE=
, ∠DOE= ,请猜想
,请猜想 与
与 之间存在什么样的数量关系,写出你的结论,并说明理由.
之间存在什么样的数量关系,写出你的结论,并说明理由. 
相关试题

