【题目】某公园的门票价格如下表所示:
购票人数 | 1~50人 | 51~100人 | 100人以上 |
每人门票价 | 20元 | 17元 | 14元 |
某校初一(1)(2)两个班去游览公园,其中(1)班人数较少,不足50人,(2)班人数较多,超过50人,但是不超过100人.如果两个班都以班为单位分别购票,则一共应付1912元;如果两个班联合起来,作为个团体购票,则只需付1456元
(1)列方程或方程组求出两个班各有多少学生?
(2)若(1)班全员参加,(2)班有20人不参加此次活动,请你设计一种最省钱方式来帮他们买票,并说明理由.
(3)你认为是否存在这样的可能:51到100人之间买票的钱数与100人以上买票的钱数相等?如果有,是多少人与多少人买票钱数相等?(直接写结果)
参考答案:
【答案】(1)初一(1)班有48人,初一(2)班有56人;(2)两个班联合起来买101张门票最省钱;理由见解析;(3)84人和102人或98人和119人买票钱数相等.
【解析】
(1)由两班人数之和为整数可得出初一(1)(2)两个班的人数之和大于100,设初一(1)班有![]() 人,初一(2)班有y人,根据总价=单价×数量,即可得出二元一次方程组,解之即可;
人,初一(2)班有y人,根据总价=单价×数量,即可得出二元一次方程组,解之即可;
(2)求出参加活动的人数,利用总价=单价×数量,分别求出购买84张门票及101张门票所需钱数,比较后即可得出结论;
(3)设m人与n人买票钱数相等(51≤m≤100,n≥101),根据总价=单价×数量且总价相等,即可得出关于m,n的二元一次方程,结合m,n为正整数及其范围,即可求出m,n的值.
(1)如果初一(1)(2)两个班的人数之和不大于100,
则1456÷17=85(人)![]() (元),不符合题意,
(元),不符合题意,
∴初一(1)(2)两个班的人数之和大于100.
设初一(1)班有x人,初一(2)班有y人,
依题意,得: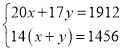 ,
,
解得:![]() ;
;
答:初一(1)班有48人,初一(2)班有56人;
(2)48+(56﹣20)=84(人).
两个班合起来买84张门票所需钱数为:84×17=1428(元),
两个班合起来买101张门票所需钱数为:101×14=1414(元),
∵1414<1428,
∴两个班合起来买101张门票最省钱;
(3)设m人与n人买票钱数相等(51≤m≤100,n≥101),
依题意,得:17m=14n,
∴m为14的整数倍,n为17的整数倍,
∴![]() 或
或![]() .
.
答:84人和102人或98人和119人买票钱数相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:我国数学家华罗庚在一次出国访问途中,看到飞机上:邻座的乘客阅读的杂志上有一道智力题,求59319的立方根,华罗庚脱口而击.众人惊命,忙问计算奥妙.你知道怎样迅速准确地计算出结果的吗?诺按照下面的分析试一试
(1)由103=1000,1003=100000,可知
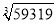 是 位数;
是 位数;(2)由59319的个位数是9,可知
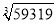 的个位数是 ;
的个位数是 ;(3)如果划去59319后面的三位319得到59,而33=27,43=64,由此确定
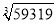 的十位数是 .
的十位数是 .请应用以上方法计算:
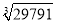 = .
= . 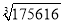 =
= -
科目: 来源: 题型:
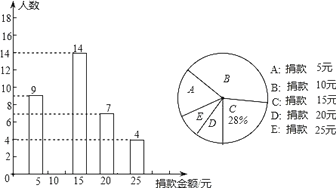
查看答案和解析>>【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示
(1)本次共抽查学生____人,并将条形图补充完整;
(2)捐款金额的众数是_____,平均数是_____;
(3)在八年级700名学生中,捐款20元及以上(含20元)的学生估计有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD交于点O,点E,点F在BD上,且 BE=DF 连接AE并延长,交BC于点G,连接CF并延长,交AD于点H.
(1)求证:△AOE≌△COF;
(2)若AC平分∠HAG,求证:四边形AGCH是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 .现点
.现点 绕着点
绕着点 以每秒
以每秒 的速度顺时针旋转一周后停止.则(1)点
的速度顺时针旋转一周后停止.则(1)点 旋转一周所用的时间是______秒;(2)同时点
旋转一周所用的时间是______秒;(2)同时点 沿线段
沿线段 自点
自点 向点
向点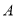 运动,假若点
运动,假若点 、
、 也能相遇,则点
也能相遇,则点 的速度是______
的速度是______ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC,BD相交于点O,∠ADB=30°,E为BC边上一点,∠AEB=45°,CF⊥BD于F.下列结论:①BE=CD,②BF=3DF,③AE=
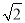 AO,④CE=CF.正确的结论有( )
AO,④CE=CF.正确的结论有( )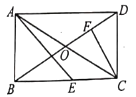
A. ①②B. ②③C. ①②④D. ①②③
-
科目: 来源: 题型:
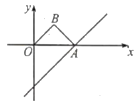
查看答案和解析>>【题目】如图,直线y=x﹣4与x轴交于点A,以OA为斜边在x轴上方作等腰Rt△OAB,并将Rt△AOB沿x轴向右平移,当点B落在直线y=x﹣4上时,Rt△OAB扫过的面积是__.
相关试题

