【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F. 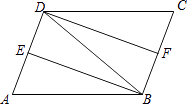
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形
AB=CD,∠A=∠C.
AB∥CD,∴∠ABD=∠CDB.
∵BE平分∠ABD,DF平分∠CDB,
∴∠ABE=∠ABD,∠CDF=∠CDB.
∴∠ABE=∠CDF.
在△ABE和△CDF中, 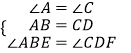
∴△ABE≌△CDF(SAS)
(2)解:四边形DFBE是矩形.理由如下:
∵AB=DB,BE平分∠ABD,
∴BE⊥AD,即∠DEB=90°.
∵AB=DB,AB=CD,
∴DB=CD.
∵DF平分∠CDB,
∴DF⊥BC,即∠BFD=90°.
在□ABCD中,∵AD∥BC,
∴∠EDF+∠DEB=180°.
∴∠EDF=90°.
∴∠DEB=∠BFD=∠EDF=90°.
∴四边形DFBE是矩形
【解析】(1)首先利用平行四边形的想得到AB=CD,∠A=∠C,再利用角平分线的性质得到∠ABE=∠CDF,利用ASA证明△ABE≌△CDF;(2)证明∠DEB=∠BFD=∠EDF=90°.即可解决问题..
-
科目: 来源: 题型:
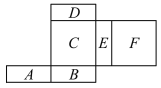
查看答案和解析>>【题目】如图是一个多面体的展开图,每个面(外表面)内部都标注了字母,请你根据要求回答问题:
(1)这个多面体是什么常见的几何体?
(2)如果D是多面体的底部,那么哪一面在上面?
(3)如果B在前面,C在左面,那么哪一面在上面?
(4)如果E在右面,F在后面,那么哪一面在上面?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把正方体的六个面分别涂上六种不同颜色,并画上朵数不等的花,各面上的颜色与花的朵数情况见下表:
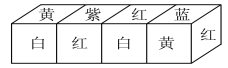
现将上述大小相同,颜色、花朵分布也完全相同的四个正方体拼成一个水平放置的长方体,如图所示.问长方体的下底面共有多少朵花?
颜色
红
黄
蓝
白
紫
绿
花的朵数
1
2
3
4
5
6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数y=
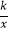 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点. 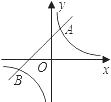
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:

对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
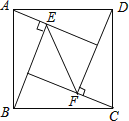
A. 7 B. 8 C. 7
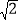 D. 7
D. 7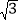
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,在ABCD中,E、F为对角线AC上的两点,且AE=CF,连接DE、BF,
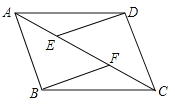
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
相关试题

