【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=﹣2.
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究: 探究一:如图1,设△PAD的面积为S,令W=tS,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;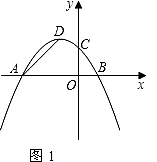
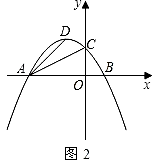
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.(参考资料:抛物线y=ax2+bx+c(a≠0)对称轴是直线x= ![]() )
)
参考答案:
【答案】
(1)解:∵抛物线y=ax2﹣x+3(a≠0)的对称轴为直线x=﹣2.
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∴D(﹣2,4)
(2)解:探究一:当0<t<4时,W有最大值.
∵抛物线 ![]() 交x轴于A、B两点,交y轴于点C,
交x轴于A、B两点,交y轴于点C,
∴A(﹣6,0),B(2,0),C(0,3),
∴OA=6,OC=3.
当0<t<4时,作DM⊥y轴于M,
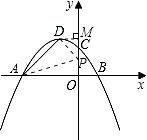
则DM=2,OM=4.
∵P(0,t),
∴OP=t,MP=OM﹣OP=4﹣t.
∵S三角形PAD=S梯形OADM﹣S三角形AOP﹣S三角形DMP
= ![]()
= ![]()
=12﹣2t
∴W=t(12﹣2t)=﹣2(t﹣3)2+18
∴当t=3时,W有最大值,W最大值=18.
探究二:
存在.分三种情况:
①当∠P1DA=90°时,作DE⊥x轴于E,
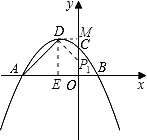
则OE=2,DE=4,∠DEA=90°,
∴AE=OA﹣OE=6﹣2=4=DE.
∴∠DAE=∠ADE=45°, ![]() ,
,
∴∠P1DE=∠P1DA﹣∠ADE=90°﹣45°=45度.
∵DM⊥y轴,OA⊥y轴,
∴DM∥OA,
∴∠MDE=∠DEA=90°,
∴∠MDP1=∠MDE﹣∠P1DE=90°﹣45°=45度.
∴P1M=DM=2, ![]() .
.
此时 ![]() ,
,
又因为∠AOC=∠P1DA=90°,
∴Rt△ADP1∽Rt△AOC,
∴OP1=OM﹣P1M=4﹣2=2,
∴P1(0,2).
∴当∠P1DA=90°时,存在点P1,使Rt△ADP1∽Rt△AOC,
此时P1点的坐标为(0,2)
②当∠P2AD=90°时,则∠P2AO=45°,
∴ ![]() ,
,
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() .
.
∴△P2AD与△AOC不相似,此时点P2不存在.
③当∠AP3D=90°时,以AD为直径作⊙O1,则⊙O1的半径 ![]() ,
,
圆心O1到y轴的距离d=4.
∵d>r,
∴⊙O1与y轴相离.
不存在点P3,使∠AP3D=90度.
∴综上所述,只存在一点P(0,2)使Rt△ADP与Rt△AOC相似.
【解析】(1)由抛物线的对称轴求出a,就得到抛物线的表达式了;(2)①下面探究问题一,由抛物线表达式找出A,B,C三点的坐标,作DM⊥y轴于M,再由面积关系:SPAD=S梯形OADM﹣SAOP﹣SDMP得到t的表达式,从而W用t表示出来,转化为求最值问题.②难度较大,运用分类讨论思想,可以分三种情况:(1)当∠P1DA=90°时;(2)当∠P2AD=90°时;(3)当AP3D=90°时;思路搞清晰问题就好解决了.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
-
科目: 来源: 题型:
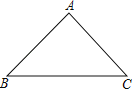
查看答案和解析>>【题目】如图,已知△ABC
(1)用直尺和圆规作△ABC的边BC上的高AD,并在线段AD上找一点E,使E到AB的距离等于ED(不写作法,保留作图痕迹);
(2)若AB=AC=5,BC=6,求出ED的长。
-
科目: 来源: 题型:
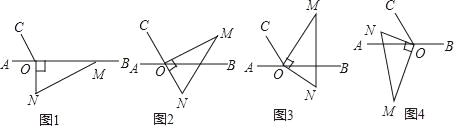
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一把直角三角尺的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角尺绕点O逆时针旋转至图2,使点N在OC的反向延长线上,请直接写出图中∠MOB的度数;
(2)将图1中的三角尺绕点O逆时针旋转至图3,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠CON的度数;
(3)将图1中的三角尺绕点O顺时针旋转至图4,使ON在∠AOC的内部,请探究∠AOM与∠NOC之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
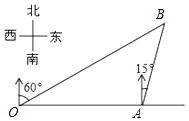
A.3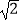 km
km
B.3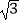 km
km
C.4 km
D.(3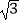 ﹣3)km
﹣3)km -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边OA、OC在坐标轴上,且OC=2OA,M、N分别为OA、OC的中点,BM与AN交于点E,若四边形EMON的面积为2,则经过点B的双曲线的解析式为( )
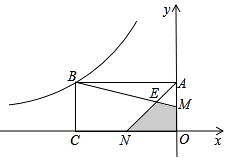
A.y=﹣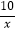
B.y=﹣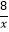
C.y=﹣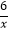
D.y=﹣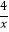
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的底边长为10cm,一腰上的中线把三角形的周长分为两部分,其中一部分比另一部分长5cm,那么这个三角形的腰长为cm.
相关试题

