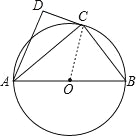
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.

参考答案:
【答案】(1) AC=4;(2)详见解析.
【解析】
试题分析:(1)首先根据直径所对的圆周角为直角得到直角三角形,然后利用勾股定理求得AC的长即可;(2)连接OC,证OC⊥CD即可;利用角平分线的性质和等边对等角,可证得∠OCA=∠CAD,即可得到OC∥AD,由于AD⊥CD,那么OC⊥CD,由此得证.
试题解析:(1)解:∵AB是⊙O直径,C在⊙O上,
∴∠ACB=90°,
又∵BC=3,AB=5,
∴由勾股定理得AC=4;
(2)证明:连接OC
∵AC是∠DAB的角平分线,
∴∠DAC=∠BAC,
又∵AD⊥DC,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴∠DCA=∠CBA,
又∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OBC=90°,
∴∠OCA+∠ACD=∠OCD=90°,
∴DC是⊙O的切线.
-
科目: 来源: 题型:
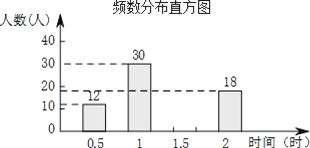
查看答案和解析>>【题目】在某市开展的“美丽春城,创卫我同行”活动中,某校倡议七年级学生利用双休日在各自社区参加义务劳动.为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制成如下不完整的统计图表:
某校七年级部分同学的劳动时间频数分布表
劳动时间(时)
频数
0.5
12
1
30
1.5
m
2
18
合计
100
(1)求m的值,并补全频数分布直方图.
(2)被调查同学劳动时间的中位数是 小时.
(3)求被调查同学的平均劳动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某书店把一本新书按标价的八折出售,仍获利20%,若该书进价为20元,则标价( )
A.24元
B.26元
C.28元
D.30元 -
科目: 来源: 题型:
查看答案和解析>>【题目】杜甫实验学校准备在操场边建一个面积为600平方米的长方形劳动实践基地.
(1)求实践基地的长y(米)关于宽x(米)的函数表达式;
(2)由于受场地限制,实践基地的宽不能超过20米,请结合实际画出函数的图象;
(3)当实践基地的宽是l5米时,实践基地的长是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:(1)2a(y-x)-3b(x-y);
(2)x3-x .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:

(1)求被抽样调查的学生有多少人?并补全条形统计图;
(2)每天户外活动时间的中位数是 小时?
(3)该校共有1850名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
249
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
A.200B.300C.400D.500
相关试题

