【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ![]() ,④S△ODC=S四边形BEOF中,正确的有( )
,④S△ODC=S四边形BEOF中,正确的有( ) 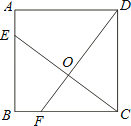
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解: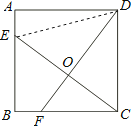
∵正方形ABCD的边长为4,
∴BC=CD=4,∠B=∠DCF=90°,
∵AE=BF=1,
∴BE=CF=4﹣1=3,
在△EBC和△FCD中,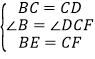
∴△EBC≌△FCD(SAS),
∴∠CFD=∠BEC,
∴∠BCE+∠BEC=∠BCE+∠CFD=90°,
∴∠DOC=90°;
故①正确;
若OC=OE,
∵DF⊥EC,
∴CD=DE,
∵CD=AD<DE(矛盾),
故②错误;
∵∠OCD+∠CDF=90°,∠CDF+∠DFC=90°,
∴∠OCD=∠DFC,
∴tan∠OCD=tan∠DFC= ![]() =
= ![]() ,
,
故③正确;
∵△EBC≌△FCD,
∴S△EBC=S△FCD ,
∴S△EBC﹣S△FOC=S△FCD﹣S△FOC ,
即S△ODC=S四边形BEOF .
故④正确.
故选C.
由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得①∠DOC=90°正确;②由线段垂直平分线的性质与正方形的性质,可得②错误;易证得∠OCD=∠DFC,即可求得③正确;由①易证得④正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=
 ,OC=
,OC= ,则另一直角边BC的长为__________.
,则另一直角边BC的长为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A是双曲线y=
 在第二象限分支上的任意一点,点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点.若四边形ABCD的面积是8,则k的值为( )
在第二象限分支上的任意一点,点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点.若四边形ABCD的面积是8,则k的值为( )
A.﹣1
B.1
C.2
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某个体水果店经营某种水果,进价
 元/千克,售价
元/千克,售价 元/千克,
元/千克, 月
月 日至
日至 月
月 日经营情况如下表:
日经营情况如下表:日期





购进





售出




损耗





 若
若 月
月 日的库存为
日的库存为 ,则
,则 月
月 日的库存为________;
日的库存为________; 就
就 月
月 日经营情况看,当天是赚还是赔了?
日经营情况看,当天是赚还是赔了? 每天交卫生费
每天交卫生费 元,则
元,则 月
月 日
日 月
月 日该个体户共赚多少钱?
日该个体户共赚多少钱? -
科目: 来源: 题型:
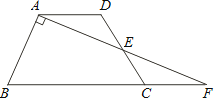
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,E是CD的中点,连接AE并延长交BC的延长线于点F,且AB⊥AE.若AB=5,AE=6,则梯形上下底之和为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某巡警骑摩托车在一条南北大道上巡逻,某天他从岗亭出发,晚上停留在
 处,规定向北方向为正,当天行驶纪录如下(单位:千米)
处,规定向北方向为正,当天行驶纪录如下(单位:千米) ,
, ,
, ,
,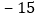 ,
, ,
, ,
, ,
,
 在岗亭何方?距岗亭多远?
在岗亭何方?距岗亭多远? 在行驶过程中,最远处离出发点有多远?
在行驶过程中,最远处离出发点有多远?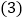 若摩托车行驶
若摩托车行驶 千米耗油
千米耗油 升,这一天共耗油多少升?
升,这一天共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体的六个面上分别标有﹣1,﹣2,﹣3,﹣4,﹣5,﹣6中的一个数,各个面上所标数字都不相同,如图是这个正方体的三种放置方法,三个正方体下底面所标数字分别是a,b,c,则a+b+c+abc= .

相关试题

