【题目】小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.

(1)小明想求出甲、乙二人在同一层楼出电梯的概率;
(2)小亮和小芳打赌说:“若甲、乙在同一层或相邻楼层出电梯,则小亮胜,否则小芳胜”.该游戏是否公平?若公平,说明理由;若不公平,请修改游戏规则,使游戏公平.
参考答案:
【答案】(1)![]() ;(2)游戏不公平,修改规则:若甲、乙同住一层或相邻楼层,则小亮得3分;小芳得5分.
;(2)游戏不公平,修改规则:若甲、乙同住一层或相邻楼层,则小亮得3分;小芳得5分.
【解析】
试题分析:(1)列表得出所有等可能的情况数,找出甲乙在同一个楼层的情况数,即可求出所求的概率;
(2)分别求出两人获胜的概率比较得到公平与否,修改规则即可.
解:(1)列表如下:
甲 乙 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
一共出现16种等可能结果,其中出现在同一层楼梯的有4种结果,
则P(甲、乙在同一层楼梯)=![]() =
=![]() ;
;
(2)由(1)列知:甲、乙住在同层或相邻楼层的有10种结果
故P(小亮胜)=P(同层或相邻楼层)=![]() =
=![]() ,P(小芳胜)=1﹣
,P(小芳胜)=1﹣![]() =
=![]() ,
,
∵![]() >
>![]() ,∴游戏不公平,
,∴游戏不公平,
修改规则:若甲、乙同住一层或相邻楼层,则小亮得3分;小芳得5分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).
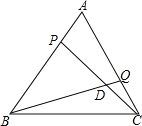
(1)AP= (用含x的式子表示);
(2)求证:△ACP≌△CBQ;
(3)求∠PDB的度数;
(4)当CP⊥AB时,直接写出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD,DE,BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥BE;④
 =1.其中正确的是( )
=1.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的三边长分别为4,5,x,则x不可能是( )
A. 3 B. 5 C. 7 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和是1800°,这个多边形是 边形,它的外角和是
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组数为三边的三角形中不是直角三角形的是
A. 9、12、15 B. 41、40、9 C. 25、7、24 D. 6、5、4
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.了解某班同学的身高情况适合用全面调查
B.数据4、5、5、6、0的平均数是5
C.数据2、3、4、2、3的中位数是4
D.甲、乙两组数据的平均数相同,方差分别是S甲2=3.2,S乙2=2.9,则甲组数据更稳定
相关试题

