【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )
A.CE= ![]() DE
DE
B.CE= ![]() DE
DE
C.CE=3DE
D.CE=2DE
参考答案:
【答案】B
【解析】解:过点D作DH⊥BC,
∵AD=1,BC=2,
∴CH=1,
DH=AB= ![]() =
= ![]() =2
=2 ![]() ,
,
∵AD∥BC,∠ABC=90°,
∴∠A=90°,
∵DE⊥CE,
∴∠AED+∠BEC=90°,
∵∠AED+∠ADE=90°,
∴∠ADE=∠BEC,
∴△ADE∽△BEC,
∴ ![]() ,
,
设BE=x,则AE=2 ![]() ,
,
即 ![]() ,
,
解得x= ![]() ,
,
∴ ![]() ,
,
∴CE= ![]() DE,
DE,
故选B.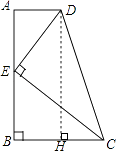
过点D作DH⊥BC,利用勾股定理可得AB的长,利用相似三角形的判定定理可得△ADE∽△BEC,设BE=x,由相似三角形的性质可解得x,易得CE,DE 的关系.本题主要考查了相似三角形的性质及判定,构建直角三角形,利用方程思想是解答此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的方程x2+(m+1)x+
 =0的一个实数根的倒数恰是它本身,则m的值是( )
=0的一个实数根的倒数恰是它本身,则m的值是( )
A.﹣
B.
C.﹣ 或
或 
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ,0)
,0)
D.(﹣ ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=
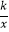 (x<0)的图象经过点A,若S△ABO=
(x<0)的图象经过点A,若S△ABO= 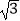 ,则k的值为 .
,则k的值为 . 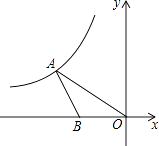
相关试题

