【题目】如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y= ![]() (x<0)的图象经过点A,若S△ABO=
(x<0)的图象经过点A,若S△ABO= ![]() ,则k的值为 .
,则k的值为 . 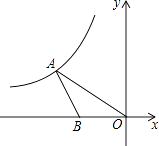
参考答案:
【答案】-3 ![]()
【解析】解:过点A作AD⊥x轴于点D,如图所示.
∵∠AOB=30°,AD⊥OD,
∴ ![]() =tan∠AOB=
=tan∠AOB= ![]() ,
,
∴设点A的坐标为(﹣3a, ![]() a).
a).
∵S△ABO= ![]() OBAD=
OBAD= ![]() ,
,
∴OB= ![]() .
.
在Rt△ADB中,∠ADB=90°,AD= ![]() a,AB=OB=
a,AB=OB= ![]() ,
,
∴BD2=AB2﹣AD2= ![]() ﹣3a2 , BD=
﹣3a2 , BD= ![]() .
.
∵OD=OB+BD=3a,即3a= ![]() +
+ ![]() ,
,
解得:a=1或a=﹣1(舍去).
∴点A的坐标为(﹣3, ![]() ),
),
∴k=﹣3× ![]() =﹣3
=﹣3 ![]() .
.
所以答案是:﹣3 ![]() .
.
【考点精析】根据题目的已知条件,利用比例系数k的几何意义的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,E是AB上一点,且DE⊥CE.若AD=1,BC=2,CD=3,则CE与DE的数量关系正确的是( )

A.CE= DE
DE
B.CE= DE
DE
C.CE=3DE
D.CE=2DE -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则BP的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 . (填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外都相同,其中红球有1个,若从中随机摸出一个球,这个球是白球的概率为
 .
.
(1)求袋子中白球的个数;(请通过列式或列方程解答)
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.

(注意:本题中的计算过程和结果均保留根号)
(1)若∠A=60°,求BC的长;
(2)若sinA= ,求AD的长.
,求AD的长.
相关试题

