【题目】“十一”黄金周的某一天,小王全家上午8时自驾小汽车从家里出发,到“番茄农庄”游玩,小汽车离家的距离![]() (千米)与小汽车离家后时间
(千米)与小汽车离家后时间![]() (时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:
(时)的关系可以用图中的折线表示,根据图像提供的有关信息,解答下列问题:

(1)“番茄农庄”离家________千米;
(2)小王全家在“番茄农庄”游玩了________小时;
(3)去时小汽车的平均速度是________千米/小时;
(4)回家时小汽车的平均速度是________千米/小时.
参考答案:
【答案】180 4 90 60
【解析】
(1)根据s轴上的最高点即可确定答案;
(2)根据s轴上不变的时间即可解答;
(3)根据去时路程除以去的时间即得答案;
(4)根据图象上14-15时所走的路程解答即可.
解:(1)由图可知:“番茄农庄”离家180千米;
(2)14-10=4小时,所以小王全家在“番茄农庄”游玩了4小时;
(3)![]() 千米/小时,所以去时小汽车的平均速度是90千米/小时;
千米/小时,所以去时小汽车的平均速度是90千米/小时;
(4)由图象可得:14-15时,汽车行驶了(180-120)=60千米,所以回家时小汽车的平均速度是60千米/小时.
故答案为:180;4;90;60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某弹簧挂上不超过20千克的物体后按一定规律伸长,测得一弹簧的长度
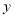 (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量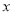 (千克)有下面的关系:
(千克)有下面的关系: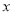
0
1
2
3
4
5
6
7
8
12
12.5
13
13.5
14
14.5
15
15.5
16
那么弹簧的总长
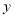 (厘米)与所挂的物体的质量
(厘米)与所挂的物体的质量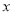 (千克)之间是否是函数关系?若是,请写出函数关系式.
(千克)之间是否是函数关系?若是,请写出函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣2,y1),(﹣5
 ,y2),(1
,y2),(1 ,y3)在函数y=2x2+8x+7的图象上,则y1,y2,y3的大小关系为_____.
,y3)在函数y=2x2+8x+7的图象上,则y1,y2,y3的大小关系为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论是___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)4(x+1)2=25;
(2)x(2x+3)=4x+6;
(3)
 ;
;(4)x2+
 =0.
=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,梯形
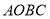 的顶点
的顶点 、
、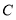 在反比例函数
在反比例函数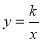 图像上,
图像上,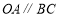 ,上底边
,上底边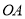 在直线
在直线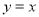 上,下底边
上,下底边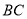 交
交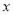 轴于
轴于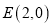 ,点
,点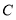 的纵坐标是1.
的纵坐标是1.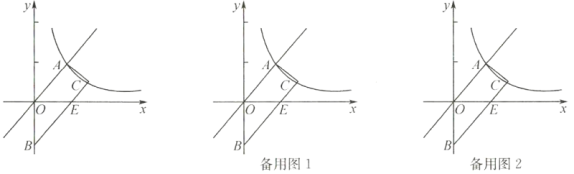
(1)求反比例函数的解析式;
(2)求四边形
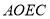 的面积;
的面积;(3)若将点
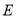 的坐标改为
的坐标改为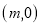 ,且
,且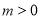 ,其他条件不变,探究四边形
,其他条件不变,探究四边形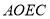 的面积;
的面积;(4)若将点
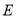 的坐标改为
的坐标改为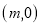 ,且
,且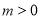 ,点
,点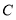 的纵坐标改为
的纵坐标改为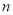 ,且
,且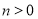 ,其他条件不变,直接写出四边形
,其他条件不变,直接写出四边形 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数的图象与x轴交于A(﹣2,0)、B(4,0)两点,且函数经过点(3,10).
(1)求二次函数的解析式;
(2)设这个二次函数的顶点为P,求△ABP的面积;
(3)当x为何值时,y≤0.(请直接写出结果)
相关试题

