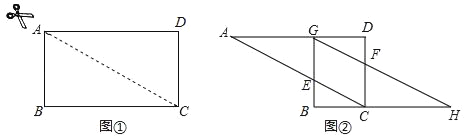
【题目】如图①,将一个长方形沿着对角线剪开即可得到两个全等的三角形,再把△ABC沿着AC方向平移,得到图②中的△GBH,BG交AC于点E,GH交CD于点F.在图②中,除△ACD与△HGB全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明.
参考答案:
【答案】△AGE≌△HCF,△EBC≌△FDG.
【解析】
本题是开放题,应先确定选择哪对三角形,再对应三角形全等条件求解.三角形全等条件中必须是三个元素,并且一定有一组对应边相等.
△AGE≌△HCF,△EBC≌△FDG.
选择证明△AGE≌△HCF,过程如下:由平移可知AG=CH.
∵△ACD与△HGB全等,
∴∠A=∠H.又BG⊥AD,DC⊥BH,
∴∠AGE=∠HCF=90°,
∴△AGE≌△HCF(ASA).
-
科目: 来源: 题型:
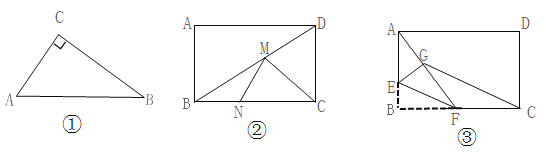
查看答案和解析>>【题目】(1)如图①,Rt△ABC中,∠C=90°,AC=3,BC=4.点D是AB边上任意一点,则CD的最小值为 。
(2)如图②,在矩形ABCD中,AB=3,BC=4.点M、N分别在BD、BC上。求CM+MN的最小值.
(3)如图③,在矩形ABCD中,AB=3,BC=4.点E是AB边上的一点,且AE=2,点F是BC边上的任意一点。把△BEF沿EF翻折,点B对应点G,连接AG、CG.四边形AGCD的面积的最小值是 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板按如图所示的方式摆放,其中△ABC为含有45°角的三角板,直线AD是等腰直角三角板的对称轴,且斜边上的点D为另一块三角板DMN的直角顶点,DM、DN分别交AB、AC于点E、F.则下列四个结论:①BD=AD=CD;②△AED≌△CFD;③BE+CF=EF;④S四边形AEDF=
 BC2.其中正确结论是_____(填序号).
BC2.其中正确结论是_____(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )

A.( ,1)
,1)
B.(1,﹣ )
)
C.(2 ,﹣2)
,﹣2)
D.(2,﹣2 )
) -
科目: 来源: 题型:
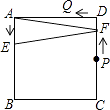
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是( )
A.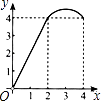
B.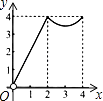
C.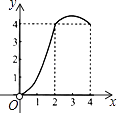
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,数轴上有点a,b,c三点

(1)用“<”将a,b,c连接起来.
(2)b﹣a 1(填“<”“>”,“=”)
(3)化简|c﹣b|﹣|c﹣a+1|+|a﹣1|
(4)用含a,b的式子表示下列的最小值:
①|x﹣a|+|x﹣b|的最小值为 ;
②|x﹣a|+|x﹣b|+|x+1|的最小值为 ;
③|x﹣a|+|x﹣b|+|x﹣c|的最小值为 .
相关试题

