【题目】数轴上点A对应的数为![]() ,点B对应的数为
,点B对应的数为![]() ,且多项式
,且多项式![]() 的二次项系数为
的二次项系数为![]() ,常数项为
,常数项为![]() .
.
(1)直接写出:![]() ;
;
(2)数轴上点A、B之间有一动点P,若点P对应的数为![]() ,试化简
,试化简![]() ;
;
(3)若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动;同时点N从点B出发,沿数轴每秒2个单位长度的速度向左移动,到达A点后立即返回并向右继续移动,求经过多少秒后,M、N两点相距1个单位长度?
参考答案:
【答案】(1)2,5;(2)x+8;(3)经过2秒或![]() 秒或7秒或8秒后,M、N两点相距1个单位长度.
秒或7秒或8秒后,M、N两点相距1个单位长度.
【解析】
(1)根据多项式的系数即可得出结论;
(2)先确定出x的范围,进而得出2x+4>0,x5<0,6x>0,最后去掉绝对值,合并即可得出结论;
(3)分点N未到达点A之前和之后,建立方程求解即可得出结论.
(1)∵多项式6x3y2xy+5的二次项系数为a,常数项为b,
∴a=2,b=5,
故答案为:2,5;
(2)∴数轴上点A对应的数为a,点B对应的数为b,
∴数轴上点A对应的数为2,点B对应的数为5,
∵数轴上点A、B之间有一动点P,点P对应的数为x,
∴2<x<5,
∴2x+4>0,x5<0,6x>0,
∴|2x+4|+2|x5||6x|=2x+42(x5)(6x)=2x+42x+106+x=x+8;
(3)设经过t秒后,M、N两点相距1个单位长度,
由运动知,AM=t,BN=2t,
①当点N到达点A之前时,
a、当M,N相遇前,M、N两点相距1个单位长度,
∴t+1+2t=5+2,
∴t=2秒,
b、当M,N相遇后,M、N两点相距1个单位长度,
∴t+2t1=5+2,
∴t=![]() 秒,
秒,
②当点N到达点A之后时,
a、当N未追上M时,M、N两点相距1个单位长度,
∴t[2t(5+2)]=1,
∴t=7秒;
b、当N追上M后时,M、N两点相距1个单位长度,
∴[2t(5+2)]t=1,
∴t=8秒;
即:经过2秒或![]() 秒或7秒或8秒后,M、N两点相距1个单位长度.
秒或7秒或8秒后,M、N两点相距1个单位长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某居民小区的一块面积为4ab平方米的长方形空地,准备在空地的四个顶点处修建一个半径为a米的扇形花台,在花台内种花,其余部分种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?

-
科目: 来源: 题型:
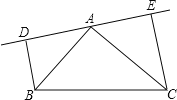
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
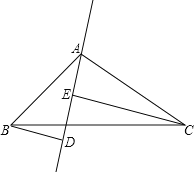
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品形状是长方形,长为8cm,它的展开图如图:
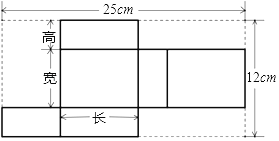
(1)求长方体的体积;
(2)请为厂家设计一种包装纸箱,使每箱能装10件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸箱的表面积尽可能小)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.

(1)求证:ΔABF≌ΔEDF;
(2)将折叠的图形恢复原状,点F与BC边上的点G正好重合,连接DG,若AB=6,BC=8,.求DG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一次数学活动课上,老师留下了这样一道题“任画一个△ABC,以BC的中点O为对称中心,作△ABC的中心对称图形,问△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.”
于是大家讨论开了,小亮说:“拼成的是平行四边形”; 小华说:“拼成的是矩形”;
小强说:“拼成的是菱形”; 小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
相关试题

