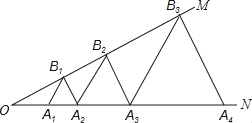
【题目】如图,∠MON=30°,点B1、B2、B3…和A1、A2、A3…分别在OM和ON上,且△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,已知OA1=1,则△A2018B2018A2019的边长为_____.
参考答案:
【答案】![]()
【解析】
首先由△A1B1A2、△A2B2A3、△A3B3A4、…分别为等边三角形,∠MON=30°,求得A1B1=OA1=1,A2B2=OA2=OA1+A1A2=2,继而可得:△A3B3A4的边长为4,△A4B4A5的边长为8,则可得规律:△AnBnAn+1的边长为:2n-1;继而求得答案.
∵△A1B1A2是等边三角形,
∴∠B1A1A2=60°,
∴∠OB1A1=∠B1A1A2∠MON=30°,
∴∠OB1A1=∠MON,
∴A1B1=OA1=1,
∴△A1B1A2的边长为1,
同理:∠OB2A2=∠MON=30°,
∴A2B2=OA2=OA1+A1A2=2,
∴△A2B2A3的边长为2,
同理可得:△A3B3A4的边长为4,△A4B4A5的边长为8,
∴△AnBnAn+1的边长为:2n1;
∴△A2018B2018A2019的边长为:22017.
故答案为:22017.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x与反比例函数y=
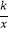 (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=  .
.
(1)求k的值.
(2)求点B的坐标.
(3)设点P(m,0),使△PAB的面积为2,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD和△ACE分别是等边三角形,AB≠AC,下列结论中正确有( )个.

⑴DC=BE,⑵∠BOD=60°,⑶∠BDO=∠CEO,⑷AO平分∠DOE,⑸AO平分∠BAC
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+bx+c交x轴于点A(﹣3,0)和点B,交y轴于点C(0,3).
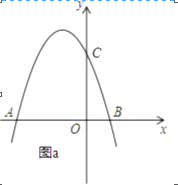
(1)求抛物线的函数表达式;
(2)若点P在抛物线上,且S△AOP=4SBOC , 求点P的坐标;
(3)如图b,设点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.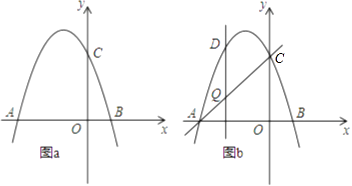
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在图中作出△ABC关于直线m对称的△A′B′C′,并写出A′、B′、C′三点的坐标(2)猜想:坐标平面内任意点P(x,y)关于直线m对称点P′的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,△ABD和△ACE分别是以AB、AC为斜边的等腰直角三角形,BE、CD相交于点F.求证:AF⊥BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如∠MON=30°、OP=6,点A、B分别在OM、ON上;(1)请在图中画出周长最小的△PAB(保留画图痕迹);(2)请求出(1)中△PAB的周长.

相关试题

