【题目】已知:如图,在△ABC中,BD、CE分别是边AC、AB上的高,点M是BC的中点,且MN⊥DE,垂足为点N
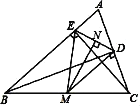
⑴求证:ME=MD;
⑵若BC=20cm,ED=12cm,求MN的长
⑶如果BD平分∠ABC,求证:AC=4EN.
参考答案:
【答案】(1)证明见解析;(2)MN=8;(3)证明见解析.
【解析】
(1)根据直角三角形的性质得到DM=![]() BC,EM=
BC,EM=![]() BC,等量代换即可证明;
BC,等量代换即可证明;
(2)由ME=MD及MN⊥DE可得MN平分ED,由勾股定理即可求得MN的长;
(3)证明△ABD≌△CBD,根据全等三角形的性质得到AD=CD,根据直角三角形的性质,等腰三角形的性质证明.
(1)∵BD是边AC上的高,
∴∠BDC=90°,
∵点M是BC的中点,
∴DM=![]() BC,
BC,
同理,EM=![]() BC,
BC,
∴ME=MD;
(2)由(1)知EM=![]() BC=10cm,
BC=10cm,
∵ME=MD,MN⊥DE,
∴EN=![]() ED=6cm,
ED=6cm,
由勾股定理得MN=![]() =8cm;
=8cm;
(3)∵BD平分∠ABC,
∴∠ABD=∠CBD,.
∵BD是边AC上的高,
∴∠ADB=∠CDB=90°.
在△ABD和△CBD中,
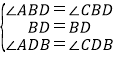 ,
,
∴△ABD≌△CBD(ASA),
∴AD=CD,
∵CE是边AB上的高,
∴∠CEA=90°,
∴AC=2ED,
∵ME=MD,MN⊥DE,
∴DE=2EN,
∴AC=4EN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有A、B、C三地,A地在B、C两地之间.甲、乙两辆汽车分别从B、C两地同时出发,沿这条公路匀速相向行驶,甲匀速行驶1小时到达A地后继续以相同的速度向C处行驶,到达C后停止,乙匀速行驶1.2小时后到达A地并停止运动,甲、乙两车离A地的距离y1、y2(千米)与行驶时间x(时)的函数关系如图所示.
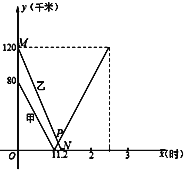
(1)BC的距离为 km
⑵求线段MN的函数表达式;
⑶求点P的坐标,并说明点P的实际意义;
⑷出发多长时间后,甲、乙相距60km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:
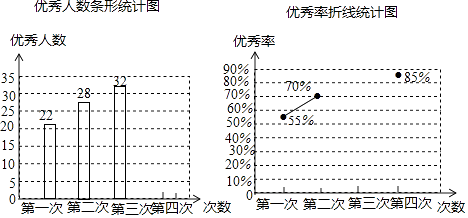
请根据以上两图解答下列问题:
(1)该班总人数是;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论. -
科目: 来源: 题型:
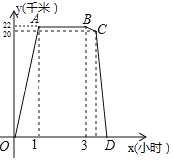
查看答案和解析>>【题目】某周日上午8:00小宇从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/小时的平均速度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原路返回.设小宇离家x(小时)后,到达离家y(千米)的地方,图中折线OABCD表示y与x之间的函数关系.
(1)活动中心与小宇家相距 千米,小宇在活动中心活动时间为 小时,他从活动中心返家时,步行用了 小时;
(2)求线段BC所表示的y(千米)与x(小时)之间的函数关系式(不必写出x所表示的范围);
(3)根据上述情况(不考虑其他因素),请判断小宇是否能在12:00前回到家,并说明理由.
-
科目: 来源: 题型:
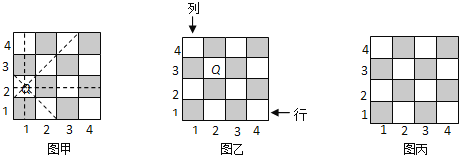
查看答案和解析>>【题目】国际象棋、中国象棋和围棋号称世界三大棋种. 国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多:“皇后”不仅能控制她所在的行与列中的每一个小方格,而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘,图中的“皇后Q”能控制图中虚线所经过的每一个小方格.
(1)在如图乙的小方格棋盘中有一“皇后Q”,她所在的位置可用“(2,3)”来表示,请说明“皇后Q”所在的位置“(2,3)”的意义,并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置.
(2)如图丙也是一个4×4的小方格棋盘,请在这个棋盘中放入四个“皇后Q”,使这四个“皇后Q”之间互不受对方控制(在图丙中的某四个小方格中标出字母Q即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB=12,弦AC=10,D是
 的中点,过点D作DE⊥AC,交AC的延长线于点E.
的中点,过点D作DE⊥AC,交AC的延长线于点E. 
(1)求证:DE是⊙O的切线;
(2)求AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在“母亲节”前期,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销售量大,店主决定将玫瑰每枝降价1元促销,降价后30元可购买玫瑰的数量是原来购买玫瑰数量的1.5倍,求降价后每枝玫瑰的售价是多少元?
相关试题

